CODIS Marker Allele Frequencies
Tina Lasisi
2024-09-16 21:02:33
Last updated: 2024-09-16
Checks: 7 0
Knit directory: PODFRIDGE/
This reproducible R Markdown analysis was created with workflowr (version 1.7.1). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20230302) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 6176bd3. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: data/.DS_Store
Ignored: output/.DS_Store
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown (analysis/CODIS-STR-freqs.Rmd) and
HTML (docs/CODIS-STR-freqs.html) files. If you’ve
configured a remote Git repository (see ?wflow_git_remote),
click on the hyperlinks in the table below to view the files as they
were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| html | bdc3293 | linmatch | 2024-07-29 | update child_distribution plot |
| Rmd | fbdfcf1 | Tina Lasisi | 2024-07-23 | Fixed allele frequency table and continued simulation development |
| html | cf281b6 | Tina Lasisi | 2024-03-03 | Build site. |
| Rmd | da5eacd | Tina Lasisi | 2024-03-03 | wflow_rename("analysis/shortrange.Rmd", "analysis/CODIS-STR-freqs.Rmd") |
| html | da5eacd | Tina Lasisi | 2024-03-03 | wflow_rename("analysis/shortrange.Rmd", "analysis/CODIS-STR-freqs.Rmd") |
CODIS marker allele frequencies
Frequencies and raw genotypes for different populations were found here and refer to Steffen, C.R., Coble, M.D., Gettings, K.B., Vallone, P.M. (2017) Corrigendum to ‘U.S. Population Data for 29 Autosomal STR Loci’ [Forensic Sci. Int. Genet. 7 (2013) e82-e83]. Forensic Sci. Int. Genet. 31, e36–e40. The US core CODIS markers are a subset of the 29 described here.
Load CODIS allele frequencies
CODIS allele frequencies were found through NIST STR base and specifically downloaded from the supplementary materials of Steffen et al 2017. These are 1036 unrelated individuals from the U.S. population.
library(readxl)
library(tidyverse)
library(data.table)
# Define the file path
file_path <- "data/1036_allelefreqs.xlsx"
# Function to map sheet names to population names
map_population_name <- function(sheet_name) {
case_when(
str_detect(sheet_name, "all") ~ "all",
str_detect(sheet_name, "AfAm") ~ "AfAm",
str_detect(sheet_name, "Cauc") ~ "Cauc",
str_detect(sheet_name, "Hispanic") ~ "Hispanic",
str_detect(sheet_name, "Asian") ~ "Asian",
TRUE ~ "Unknown"
)
}
# Function to read each sheet and process the data
read_and_process_sheet <- function(sheet) {
df <- read_excel(file_path, sheet = sheet, range = "A5:AD101", col_names = FALSE)
colnames(df) <- c("allele", "CSF1PO", "D10S1248", "D12S391", "D13S317", "D16S539", "D18S51", "D19S433", "D1S1656",
"D21S11", "D22S1045", "D2S1338", "D2S441", "D3S1358", "D5S818", "D6S1043", "D7S820", "D8S1179",
"F13A01", "F13B", "FESFPS", "FGA", "LPL", "Penta_C", "Penta_D", "Penta_E", "SE33", "TH01", "TPOX", "vWA")
df <- df %>%
mutate(allele = as.character(allele)) %>%
pivot_longer(-allele, names_to = "marker", values_to = "frequency") %>%
mutate(population = map_population_name(sheet)) %>%
replace_na(list(frequency = 0))
return(df)
}
# Read all sheets into a list of dataframes and combine them
sheet_names <- excel_sheets(file_path)
sheets_data <- lapply(sheet_names, read_and_process_sheet)
df_allelefreq <- bind_rows(sheets_data)
# Convert to data.table
setDT(df_allelefreq)
# Print the combined dataframe to check
print(head(df_allelefreq)) allele marker frequency population
<char> <char> <num> <char>
1: 2.2 CSF1PO 0 all
2: 2.2 D10S1248 0 all
3: 2.2 D12S391 0 all
4: 2.2 D13S317 0 all
5: 2.2 D16S539 0 all
6: 2.2 D18S51 0 all# Check if the population column is correct
print(unique(df_allelefreq$population))[1] "all" "AfAm" "Cauc" "Hispanic" "Asian" # Save the combined dataframe to a single CSV file
fwrite(df_allelefreq, "data/df_allelefreq_combined.csv")
# Function to sort alleles numerically while treating them as characters
sort_alleles <- function(df) {
df %>%
mutate(allele = as.numeric(allele)) %>%
arrange(allele) %>%
mutate(allele = as.character(allele))
}
# Create and save a dataframe per population with alleles as the first column and markers as subsequent columns
populations <- unique(df_allelefreq$population)
for (pop in populations) {
df_pop <- df_allelefreq[population == pop] %>%
pivot_wider(names_from = marker, values_from = frequency) %>%
sort_alleles()
fwrite(df_pop, paste0("data/1036_", pop, "_wide.csv"))
}
# Create the wide-format dataframe for all populations
df_allelefreq_wide <- df_allelefreq %>%
pivot_wider(names_from = population, values_from = frequency) %>%
replace_na(list(all = 0, AfAm = 0, Cauc = 0, Hispanic = 0, Asian = 0))
# Convert to data.table
setDT(df_allelefreq_wide)
# Sort the wide dataframe alleles numerically
df_allelefreq_wide <- sort_alleles(df_allelefreq_wide)
# Print the wide dataframe to check
# print(head(df_allelefreq_wide))
# Save the wide-format dataframe to a CSV file
fwrite(df_allelefreq_wide, "data/df_allelefreq_wide.csv")
# Convert allele to numeric in the df_allelefreq table
df <- copy(df_allelefreq)
df[, allele := as.numeric(allele)]
# Print the modified dataframe to check
# print(head(df))
#
# # Filter out rows where frequency is 0
df<- df %>%
filter(frequency != 0)Box plot of allele frequencies
Below we show a box plot of the distribution of allele frequencies for each marker, grouped by population.
df %>%
group_by(population) %>%
filter(population != "all") %>%
ggplot(aes(x = marker, y = allele, fill = population)) +
geom_boxplot() +
labs(x = "Marker", y = "Allele",
title = "Range of Alleles Across Different Markers (Grouped by Population)") +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))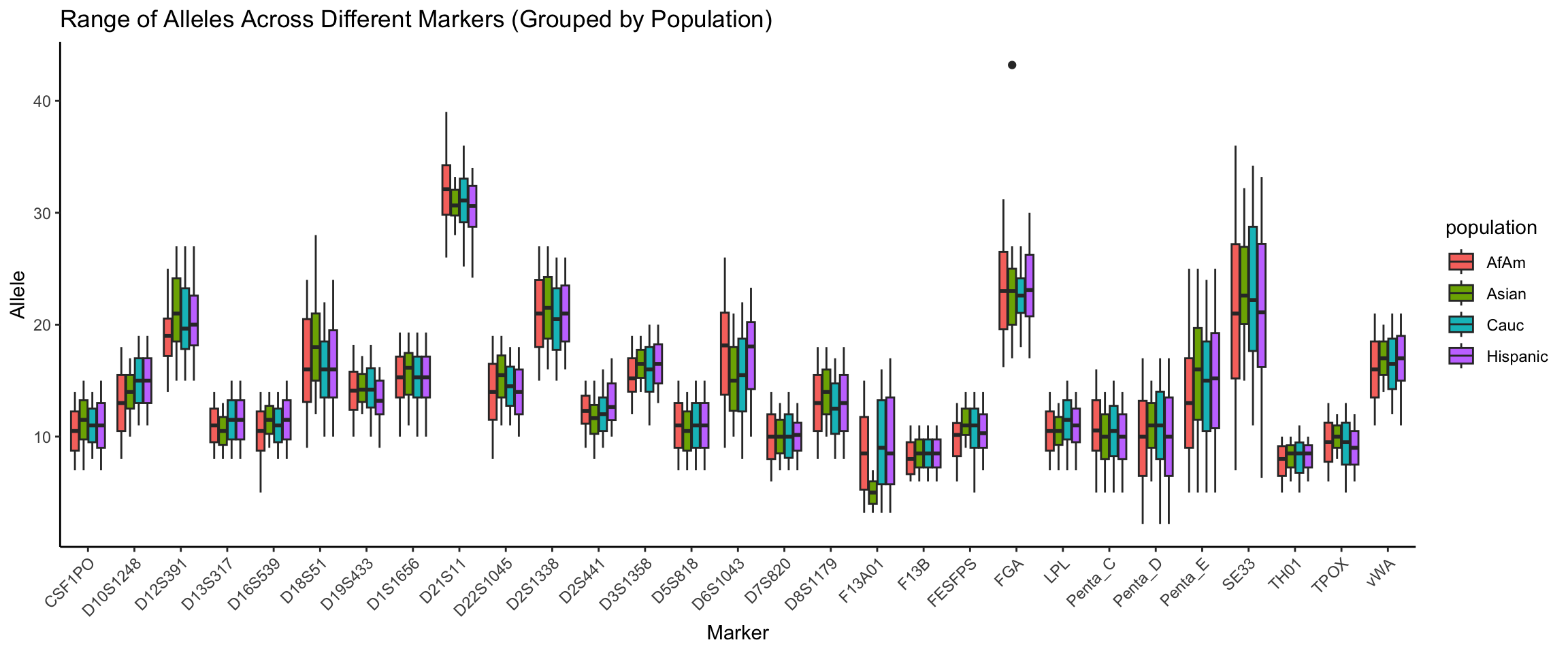
| Version | Author | Date |
|---|---|---|
| cf281b6 | Tina Lasisi | 2024-03-03 |
Histogram of allele frequencies
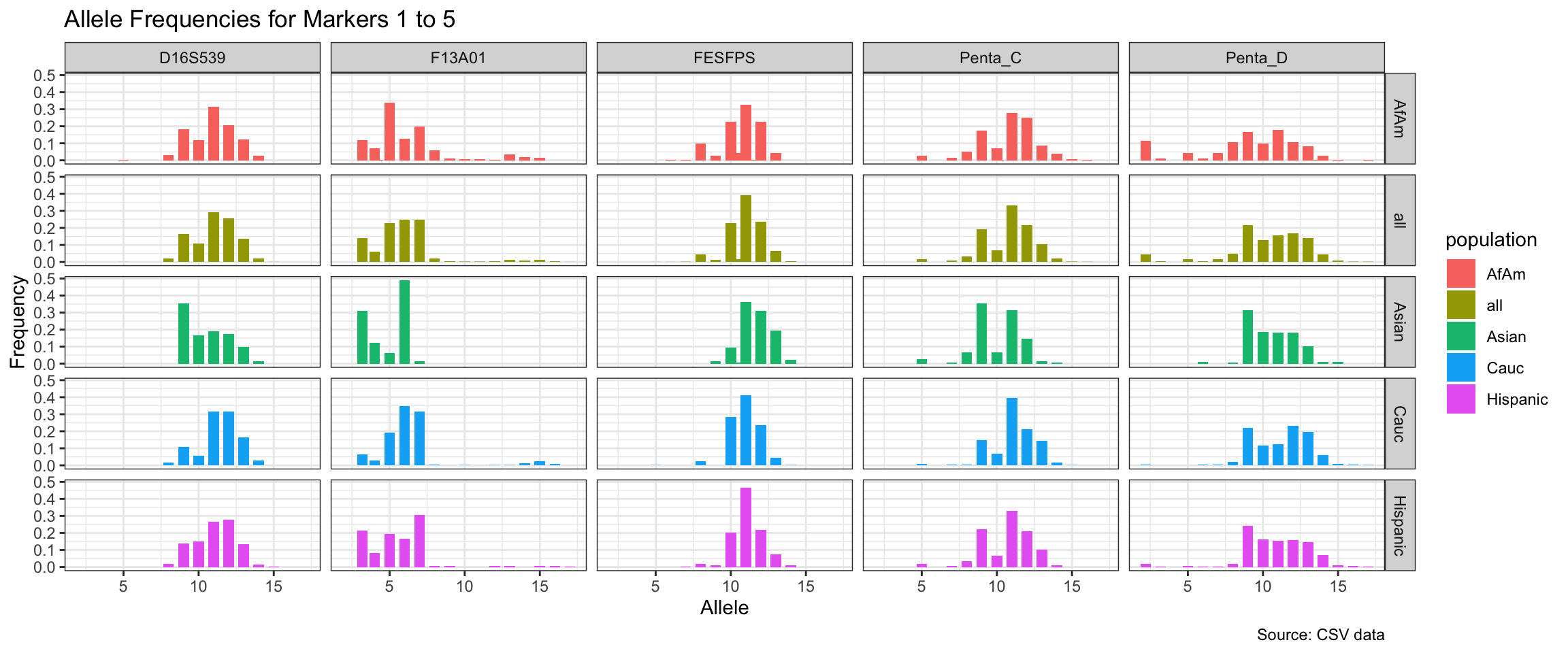
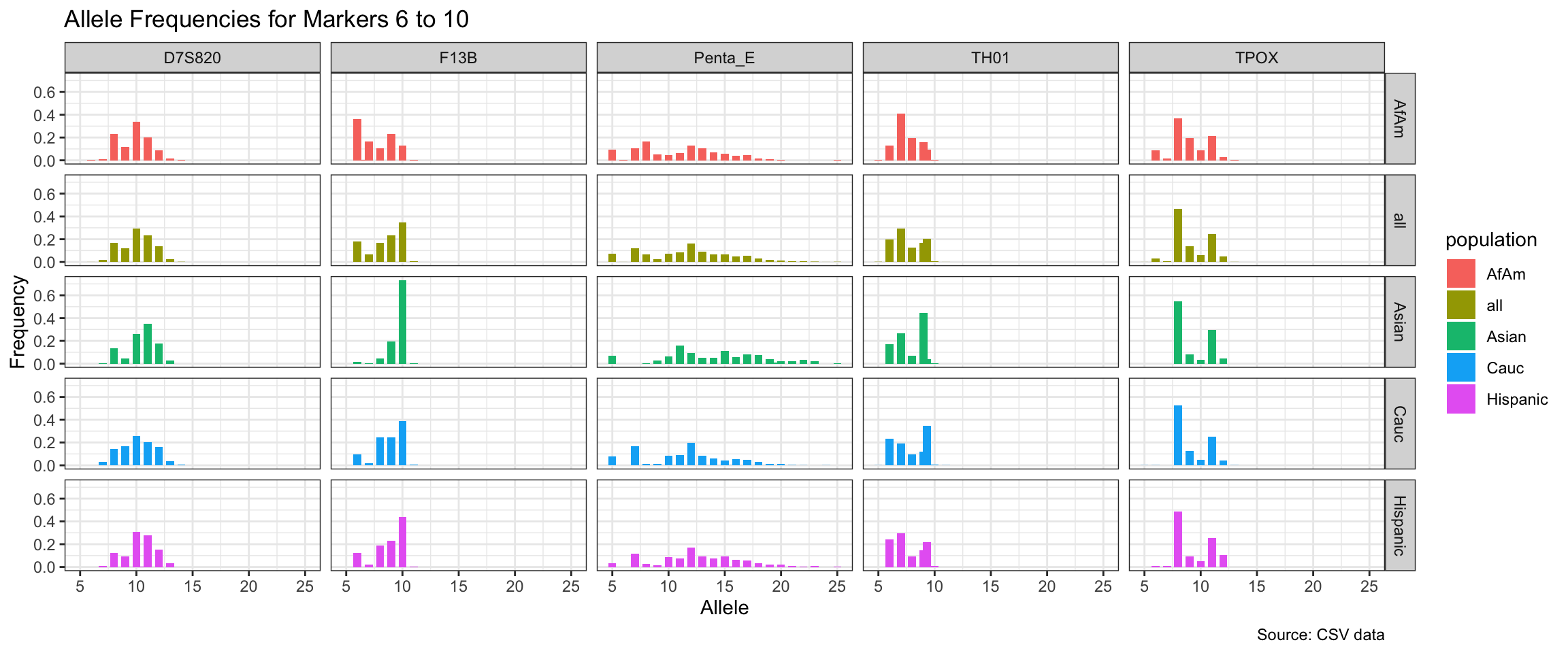
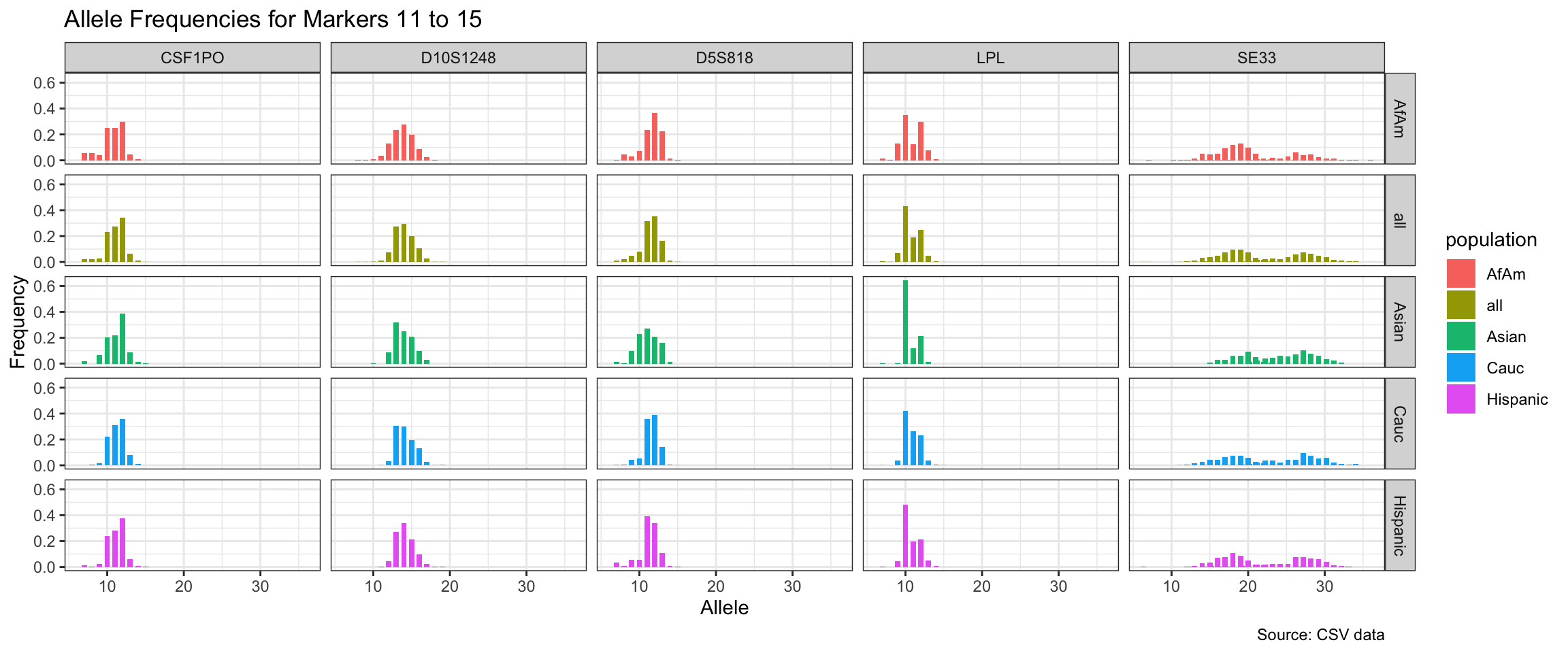
Below we show a histogram of the distribution of allele frequencies for each marker, grouped by population.
# Find unique markers and split them into chunks of 5
unique_markers <- unique(df$marker)
marker_chunks <- split(unique_markers, ceiling(seq_along(unique_markers)/5))
# Loop through the chunks and create a plot for each chunk
for(i in seq_along(marker_chunks)) {
df_chunk <- df %>% filter(marker %in% marker_chunks[[i]])
p <- ggplot(df_chunk, aes(x = allele, y = frequency, fill = population)) +
geom_col(position = "dodge", width = 0.7) +
facet_grid(population ~ marker) +
# scale_x_continuous(breaks = seq(2.2, 43.2, by = 1)) +
labs(x = "Allele", y = "Frequency",
title = paste("Allele Frequencies for Markers", i*5-4, "to", min(i*5, length(unique_markers))),
caption = "Source: CSV data") +
theme_bw()
print(p)
}
| Version | Author | Date |
|---|---|---|
| cf281b6 | Tina Lasisi | 2024-03-03 |
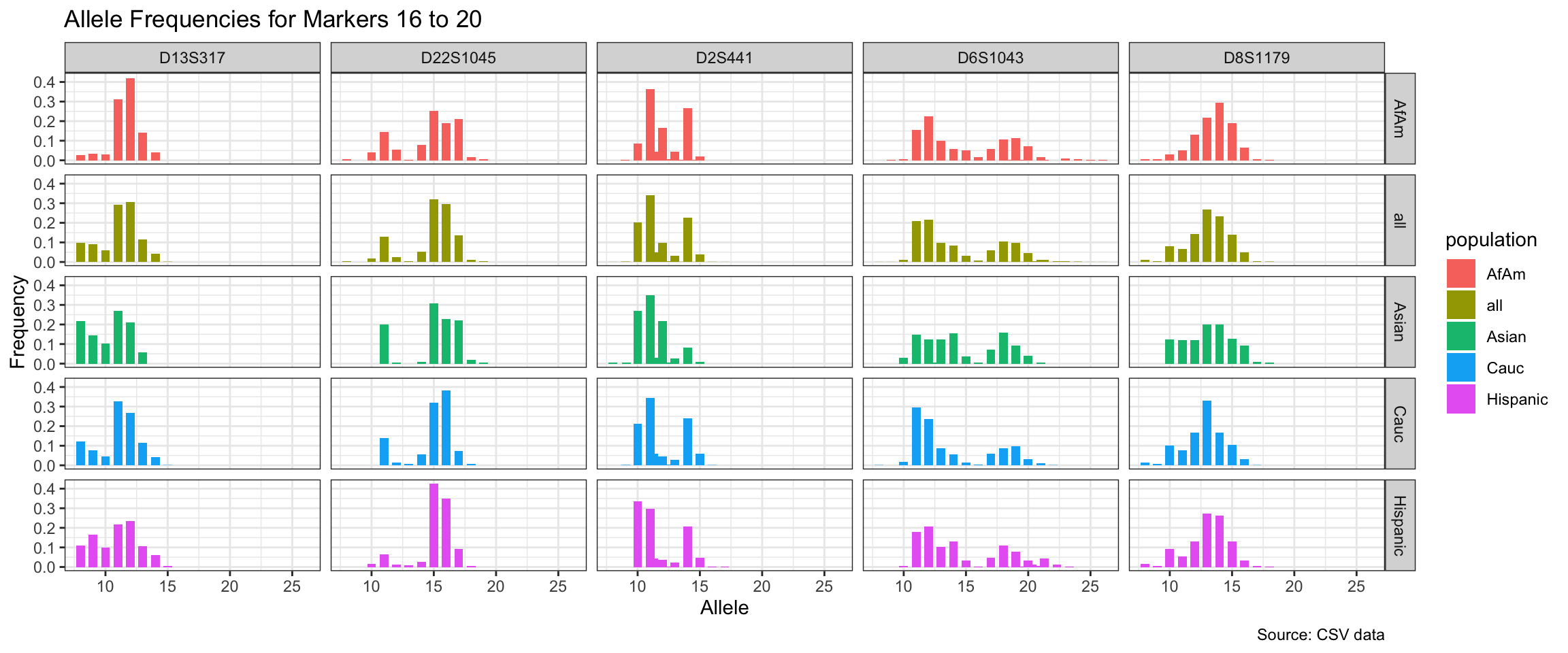
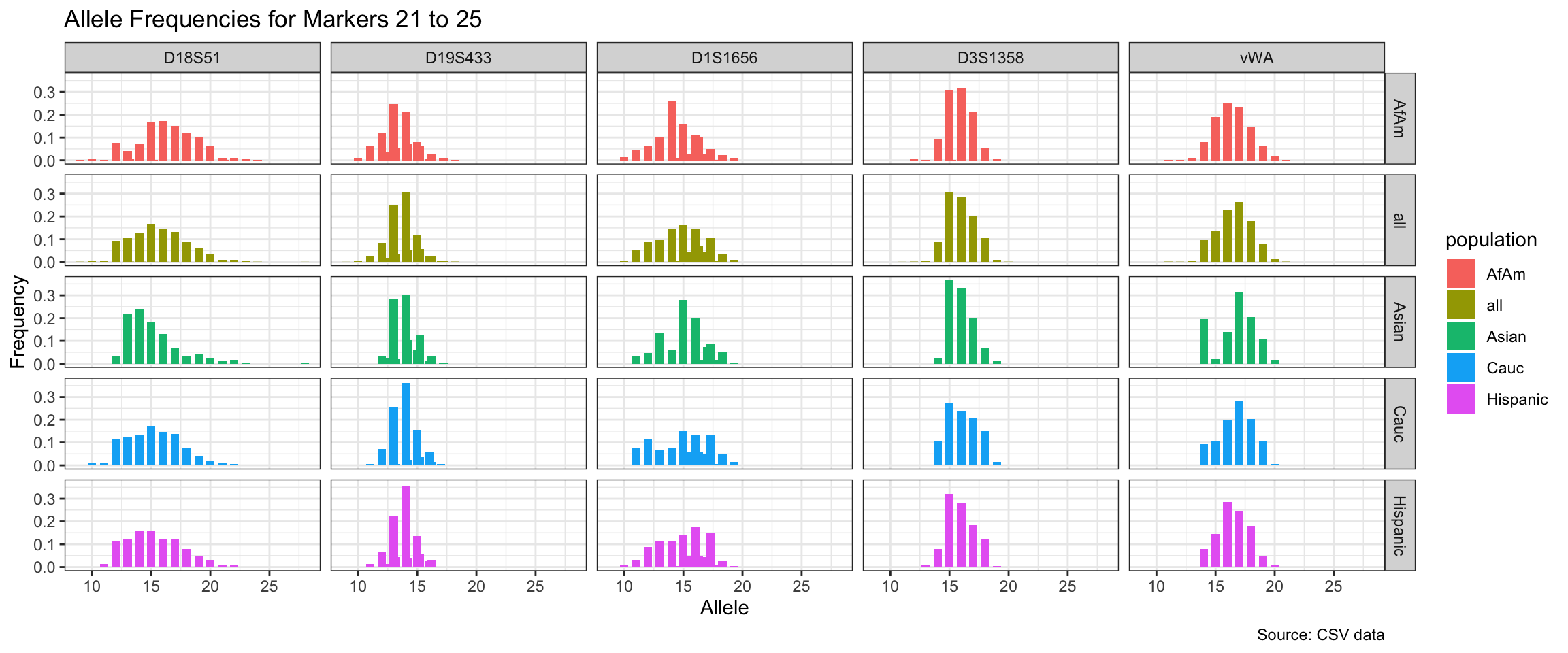
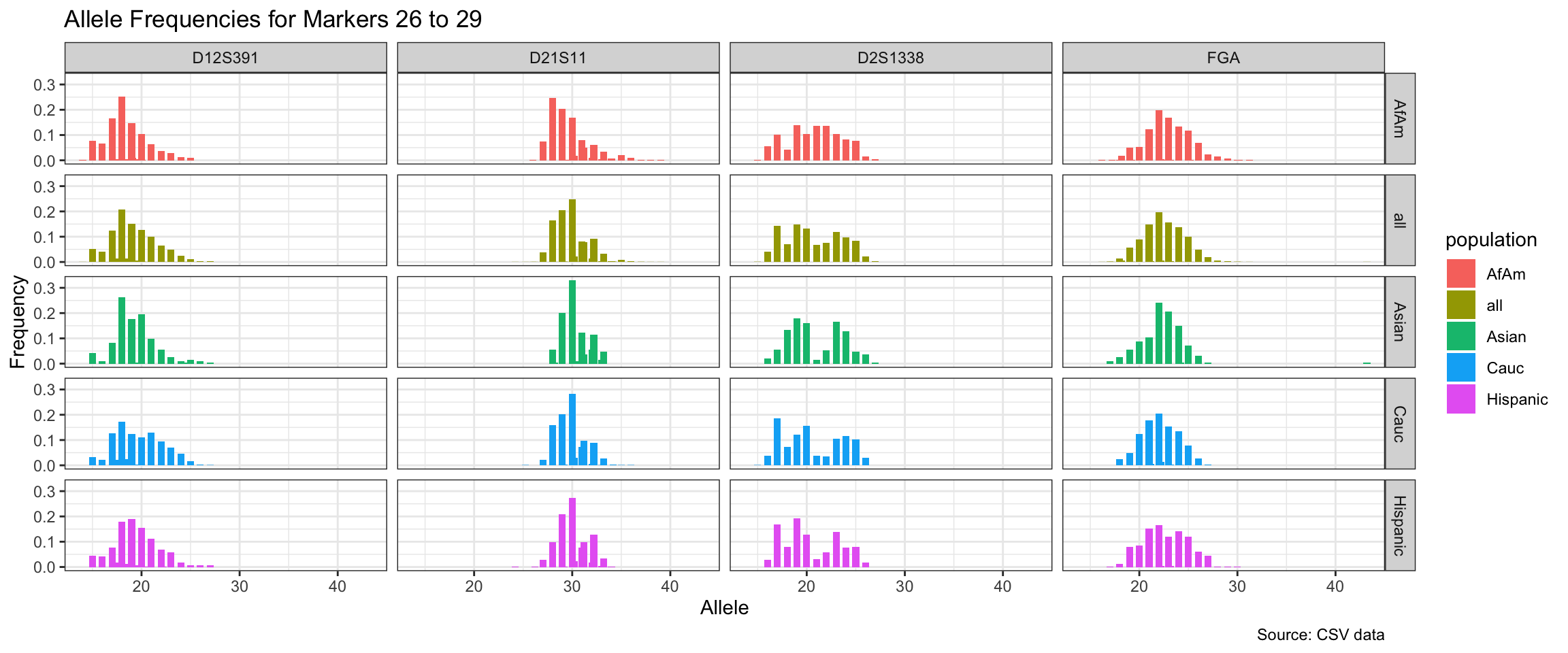
| Version | Author | Date |
|---|---|---|
| cf281b6 | Tina Lasisi | 2024-03-03 |
Summary of allele frequencies
summary_df <- df %>%
group_by(marker, population) %>%
summarise(num_alleles = n_distinct(allele))library(knitr)
library(kableExtra)
summary_df <- df %>%
group_by(marker, population) %>%
summarise(num_alleles = n_distinct(allele), .groups = 'drop')
summary_pivot <- summary_df %>%
pivot_wider(names_from = population, values_from = num_alleles)
# Print the table using kable and kableExtra for styling
summary_pivot %>%
kable("markdown", caption = "Summary of Distinct Alleles by Marker and Population") %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))| marker | AfAm | Asian | Cauc | Hispanic | all |
|---|---|---|---|---|---|
| CSF1PO | 8 | 8 | 7 | 9 | 9 |
| D10S1248 | 11 | 7 | 9 | 9 | 12 |
| D12S391 | 19 | 15 | 16 | 19 | 24 |
| D13S317 | 7 | 6 | 8 | 8 | 8 |
| D16S539 | 8 | 6 | 7 | 8 | 9 |
| D18S51 | 19 | 13 | 15 | 15 | 22 |
| D19S433 | 14 | 11 | 15 | 13 | 16 |
| D1S1656 | 15 | 12 | 15 | 15 | 15 |
| D21S11 | 20 | 12 | 16 | 16 | 27 |
| D22S1045 | 11 | 8 | 8 | 9 | 11 |
| D2S1338 | 13 | 12 | 12 | 11 | 13 |
| D2S441 | 11 | 10 | 11 | 10 | 15 |
| D3S1358 | 9 | 6 | 9 | 8 | 11 |
| D5S818 | 9 | 8 | 9 | 9 | 9 |
| D6S1043 | 20 | 13 | 14 | 18 | 27 |
| D7S820 | 9 | 7 | 9 | 8 | 11 |
| D8S1179 | 11 | 9 | 10 | 11 | 11 |
| F13A01 | 14 | 5 | 12 | 12 | 16 |
| F13B | 7 | 6 | 6 | 6 | 7 |
| FESFPS | 10 | 7 | 7 | 9 | 12 |
| FGA | 23 | 13 | 14 | 16 | 27 |
| LPL | 8 | 6 | 8 | 7 | 9 |
| Penta_C | 12 | 9 | 10 | 9 | 12 |
| Penta_D | 15 | 9 | 13 | 15 | 16 |
| Penta_E | 17 | 19 | 19 | 20 | 23 |
| SE33 | 41 | 22 | 39 | 36 | 53 |
| TH01 | 7 | 6 | 8 | 6 | 8 |
| TPOX | 8 | 5 | 8 | 7 | 9 |
| vWA | 11 | 7 | 10 | 9 | 11 |
Simulating genotypes
One marker at a time
# Function to simulate genotypes for a pair of individuals
simulate_genotypes <- function(allele_frequencies, relationship_type) {
# Draw two alleles for the first individual from the population allele frequencies
individual1 <- sample(names(allele_frequencies), size = 2, replace = TRUE, prob = allele_frequencies)
# Define the probabilities of sharing 0, 1, or 2 IBD alleles for each relationship type
relationship_probs <- list(
'parent_child' = c(0, 1, 0), # In a parent-child relationship, always 1 allele is shared
'full_siblings' = c(1/4, 1/2, 1/4), # For full siblings, the probabilities are 1/4 for sharing 0, 1/2 for sharing 1, and 1/4 for sharing 2 alleles
'half_siblings' = c(1/2, 1/2, 0), # For half siblings, the probabilities are 1/2 for sharing 0 and 1/2 for sharing 1 allele
'cousins' = c(7/8, 1/8, 0), # For cousins, the probabilities are 7/8 for sharing 0 and 1/8 for sharing 1 allele
'second_cousins' = c(15/16, 1/16, 0), # For second cousins, the probabilities are 15/16 for sharing 0 and 1/16 for sharing 1 allele
'unrelated' = c(1, 0, 0) # For unrelated individuals, they always share 0 alleles
)
# Get the probabilities of sharing alleles for the specific relationship type
prob_shared_alleles <- relationship_probs[[relationship_type]]
# Draw the number of shared alleles based on these probabilities
num_shared_alleles <- sample(c(0, 1, 2), size = 1, prob = prob_shared_alleles)
# Construct the genotype of the second individual by sampling the shared alleles from the first individual
# and the rest from the population allele frequencies
individual2 <- c(sample(individual1, size = num_shared_alleles), sample(names(allele_frequencies), size = 2 - num_shared_alleles, replace = TRUE, prob = allele_frequencies))
# Return the genotypes of the two individuals and the number of shared alleles
return(list(individual1 = individual1, individual2 = individual2, num_shared_alleles = num_shared_alleles))
}
# Function to calculate the index of relatedness
calculate_relatedness <- function(simulated_genotypes, allele_frequencies) {
# Calculate the number of alleles that the two individuals share
num_shared_alleles <- sum(simulated_genotypes$individual1 %in% simulated_genotypes$individual2)
# Calculate the index of relatedness as the number of shared alleles divided by the sum of the inverse of allele frequencies
# of the alleles in the genotypes of both individuals. This gives a higher weight to rare alleles.
relatedness <- num_shared_alleles / (sum(1 / allele_frequencies[simulated_genotypes$individual1]) + sum(1 / allele_frequencies[simulated_genotypes$individual2]))
# Return the index of relatedness and the number of shared alleles
return(list(relatedness = relatedness, num_shared_alleles = simulated_genotypes$num_shared_alleles))
}
# Function to simulate genotypes and calculate relatedness for different relationships
simulate_relatedness <- function(df, marker, population, relationship_type) {
# Filter the data frame to get the allele frequencies for the specific marker and population
allele_frequencies <- df %>%
filter(marker == marker, population == population) %>%
pull(frequency) %>%
setNames(df$allele)
# Simulate the genotypes for the pair of individuals using these allele frequencies and the specific relationship type
simulated_genotypes <- simulate_genotypes(allele_frequencies, relationship_type)
# Calculate the relatedness index based on these simulated genotypes and the allele frequencies
relatedness_data <- calculate_relatedness(simulated_genotypes, allele_frequencies)
# Return the marker, population, relationship type, and the calculated relatedness data
return(c(list(marker = marker, population = population, relationship_type = relationship_type), relatedness_data))
}
# Example usage
simulate_relatedness(df, marker = "F13A01", population = "Asian", relationship_type = "full_siblings")$marker
[1] "F13A01"
$population
[1] "Asian"
$relationship_type
[1] "full_siblings"
$relatedness
[1] 0
$num_shared_alleles
[1] 0simulate_all_relationships <- function(df, num_simulations) {
# Define the list of relationship types
relationship_types <- c('parent_child', 'full_siblings', 'half_siblings', 'cousins', 'second_cousins', 'unrelated')
# Initialize an empty list to store results
results <- list()
# Iterate over all combinations of markers, populations, and relationship types
for (marker in unique(df$marker)) {
for (population in unique(df$population)) {
for (relationship_type in relationship_types) {
for (i in 1:num_simulations) {
# Simulate relatedness and add the result to the list
results[[length(results) + 1]] <- simulate_relatedness(df, marker, population, relationship_type)
}
}
}
}
# Convert the list of results to a dataframe
results_df <- do.call(rbind, lapply(results, function(x) as.data.frame(t(unlist(x)))))
return(results_df)
}# Usage:
# df <- # Your dataframe here
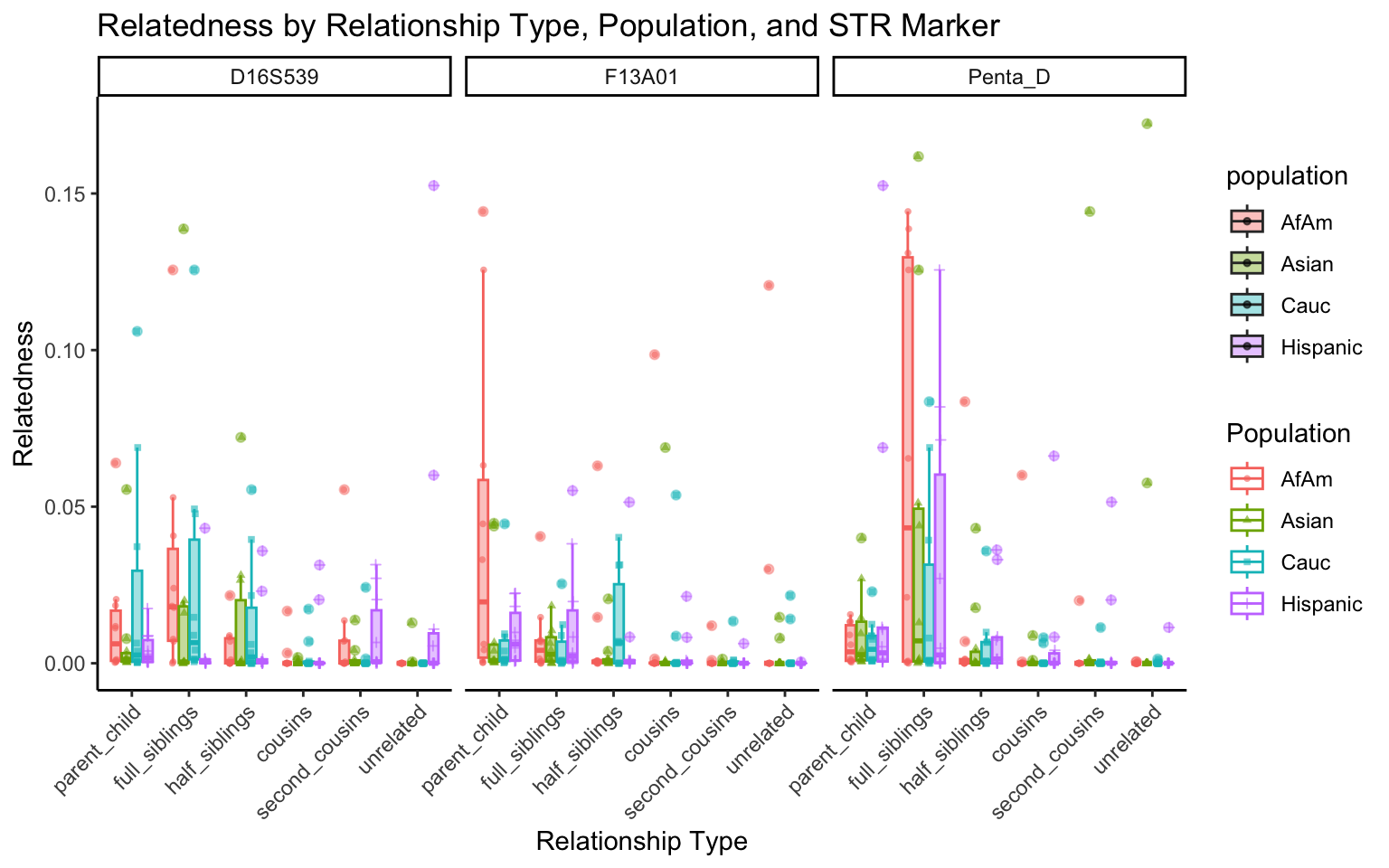
results_df <- simulate_all_relationships(df, num_simulations = 10)Visualization
# Function to capitalize the first letter of a string
ucfirst <- function(s) {
paste(toupper(substring(s, 1,1)), substring(s, 2), sep = "")
}
create_plot <- function(df, variable_to_plot) {
# Create the plot
p <- ggplot(df, aes(x = relationship_type, y = .data[[variable_to_plot]], color = population, shape = population, fill = population)) +
geom_boxplot(alpha = 0.4) + # Change the order of geom_boxplot() and geom_point() and adjust alpha
geom_point(position = position_jitterdodge(jitter.width = 0.1, dodge.width = 0.75), size = 1, alpha = 0.6) +
facet_grid(. ~ marker) +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
scale_x_discrete(limits = c('parent_child', 'full_siblings', 'half_siblings', 'cousins', 'second_cousins', 'unrelated')) +
labs(title = paste(ucfirst(variable_to_plot), "by Relationship Type, Population, and STR Marker"),
x = "Relationship Type",
y = ucfirst(variable_to_plot),
color = "Population",
shape = "Population")
return(p)
}# Filter your data for the first 3 unique STR markers
factor_vars <- c("marker", "population", "relationship_type")
numeric_vars <- c("relatedness", "num_shared_alleles")
# Filter your data for unique STR markers and remove the "all" population
results_df_filtered <- results_df %>%
filter(population != "all") %>%
mutate(
across(all_of(factor_vars), as.factor),
across(all_of(numeric_vars), as.numeric)
)
# Find the total number of unique markers
total_markers <- length(unique(results_df_filtered$marker))
# Iterate through the unique markers in groups of 3
for (i in seq(1, total_markers, by = 3)) {
# Filter the data for the current set of 3 or fewer markers
filtered_results_df <- results_df_filtered %>%
filter(marker %in% unique(marker)[i:min(i+2, total_markers)])
# Create and display the plots for the current set of markers
for (variable_to_plot in c("relatedness", "num_shared_alleles")) {
plot <- create_plot(df = filtered_results_df, variable_to_plot = variable_to_plot)
print(plot) # Print the plot to display it in the RMarkdown document
}
}
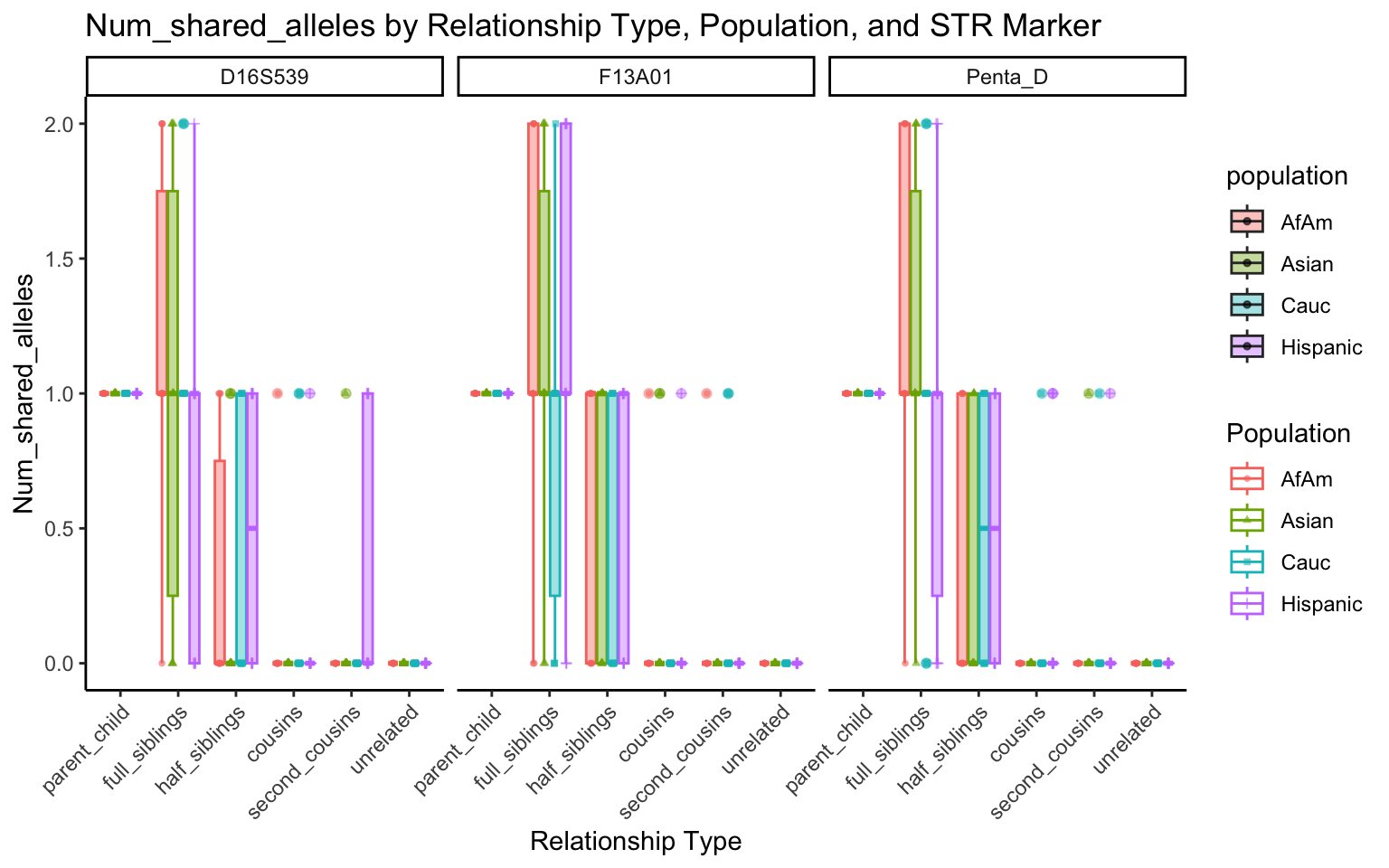
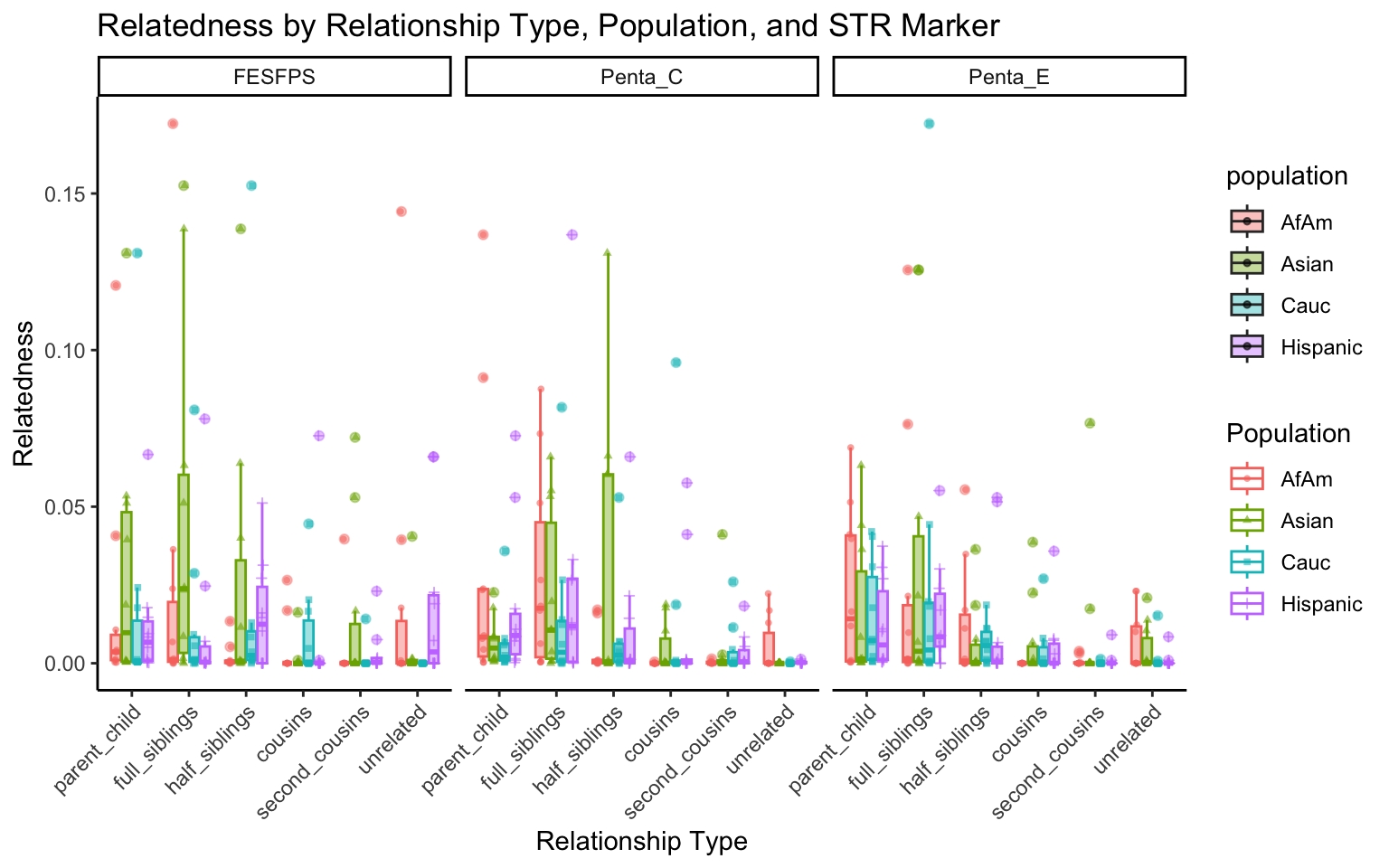
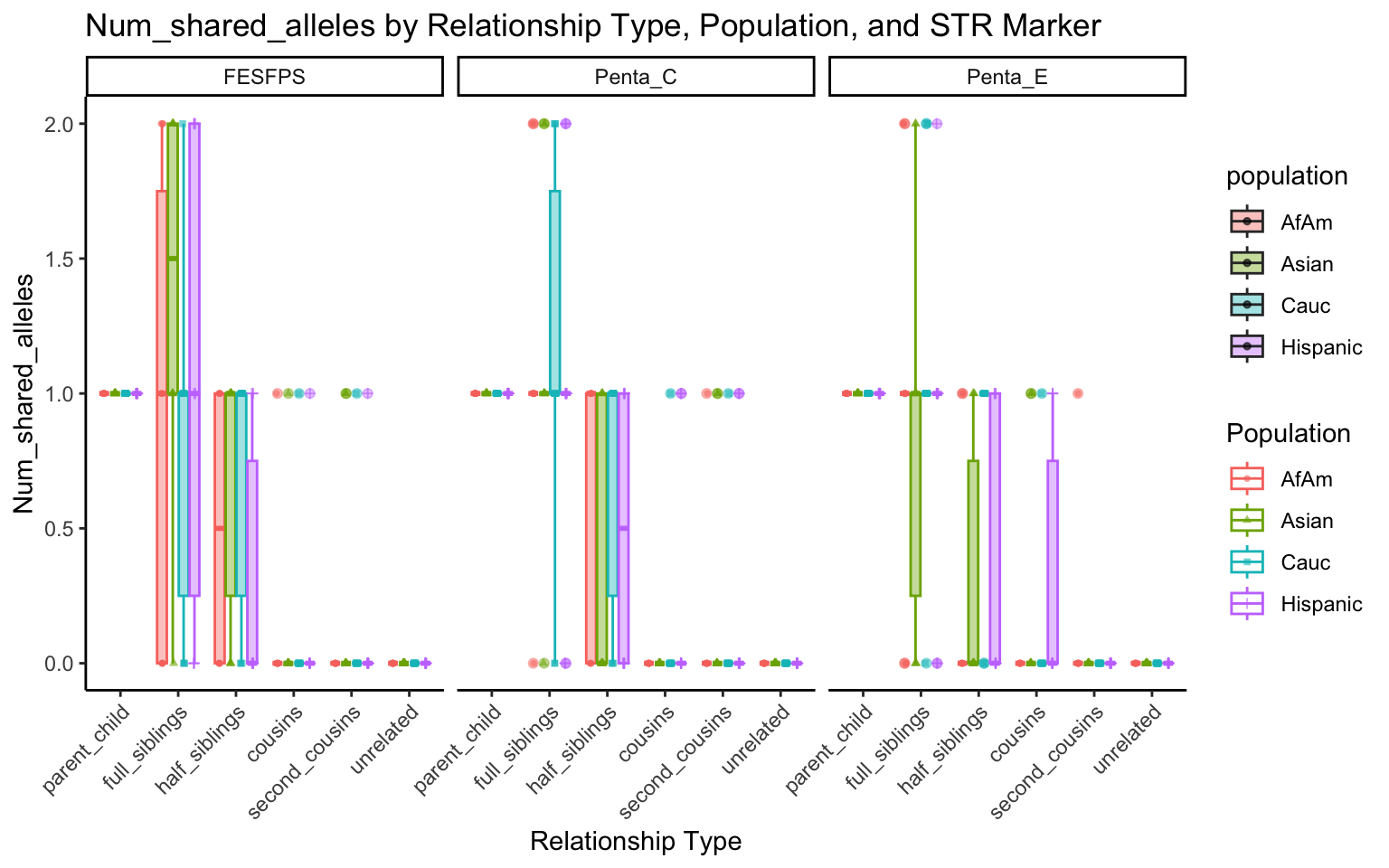
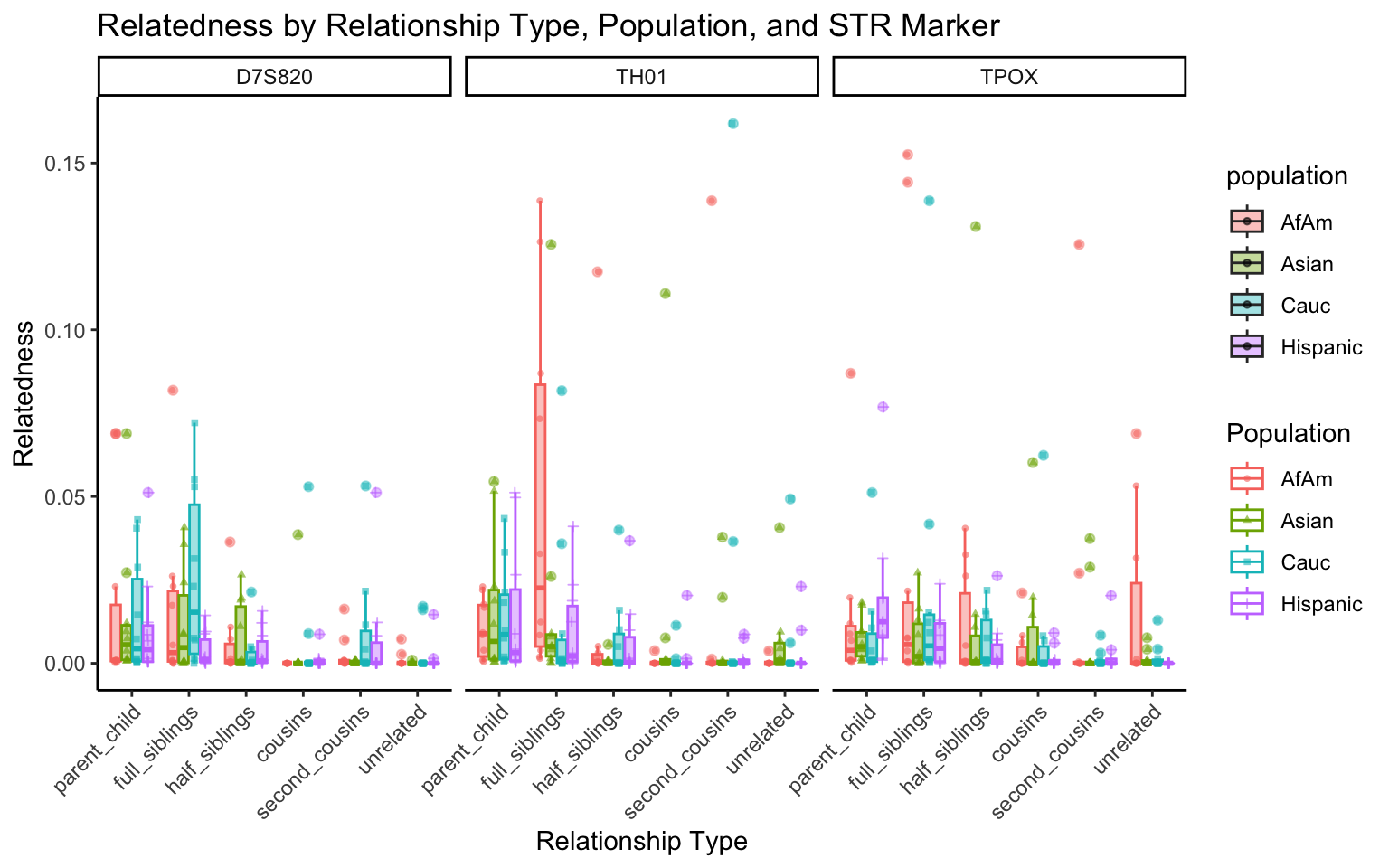
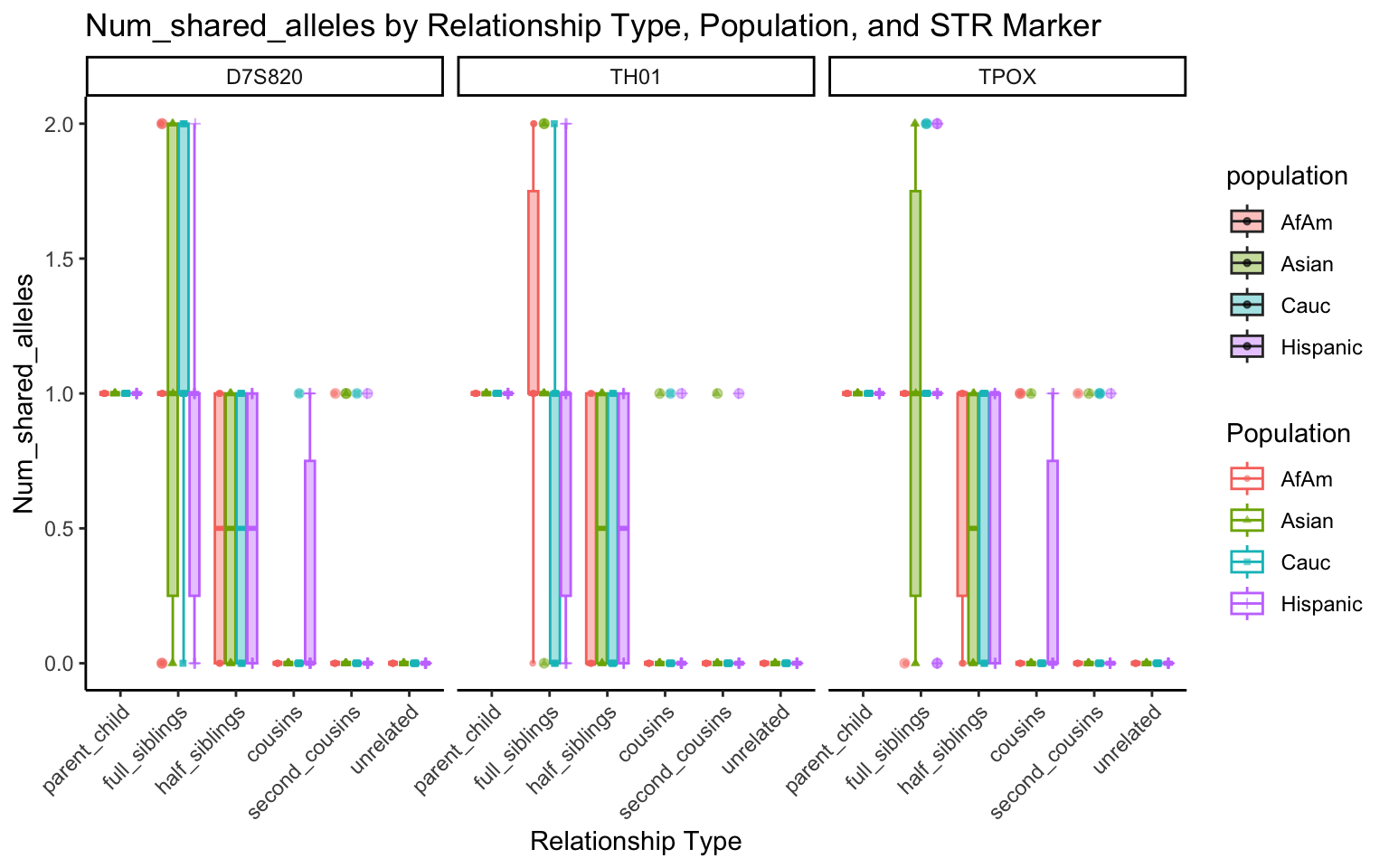
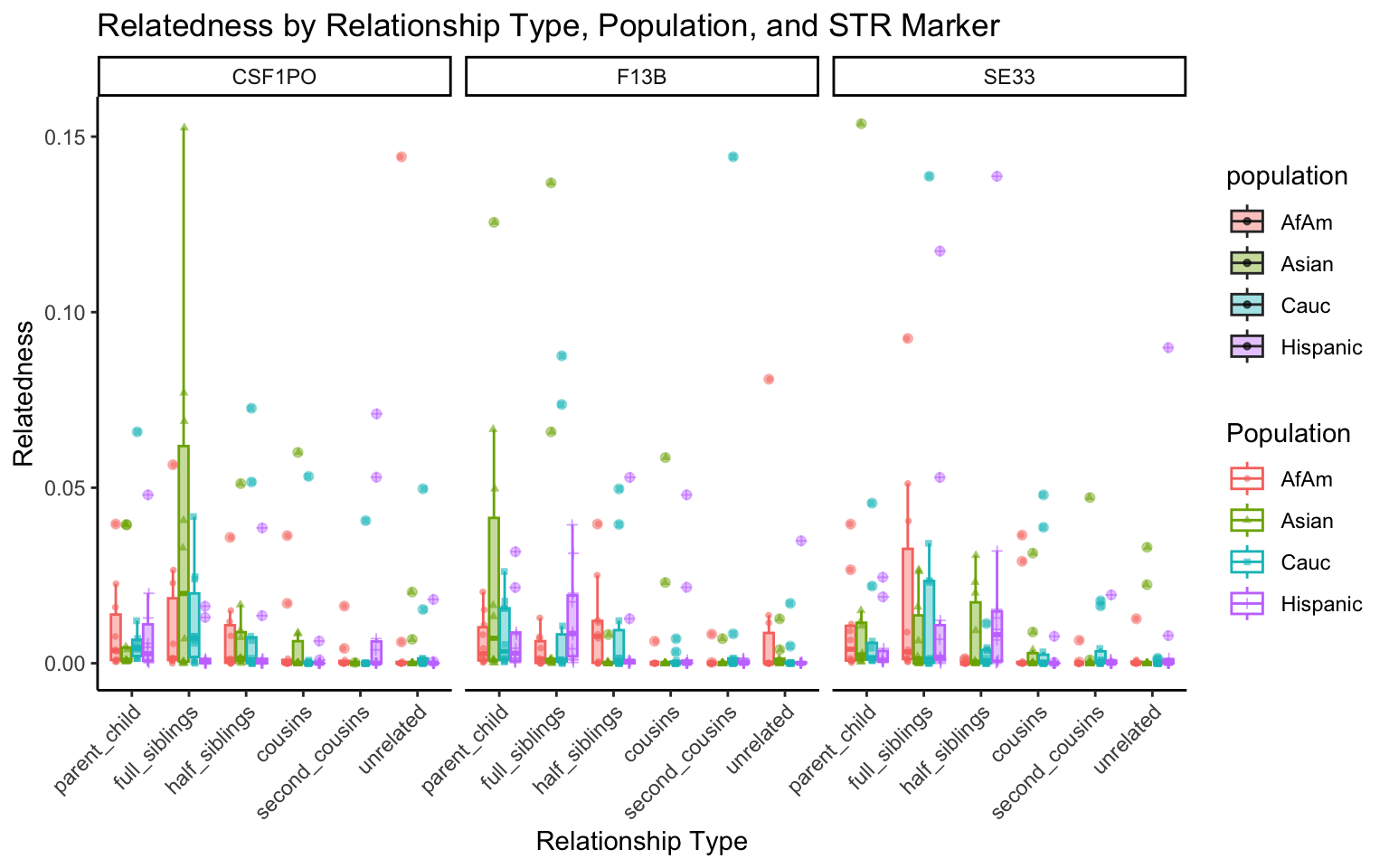
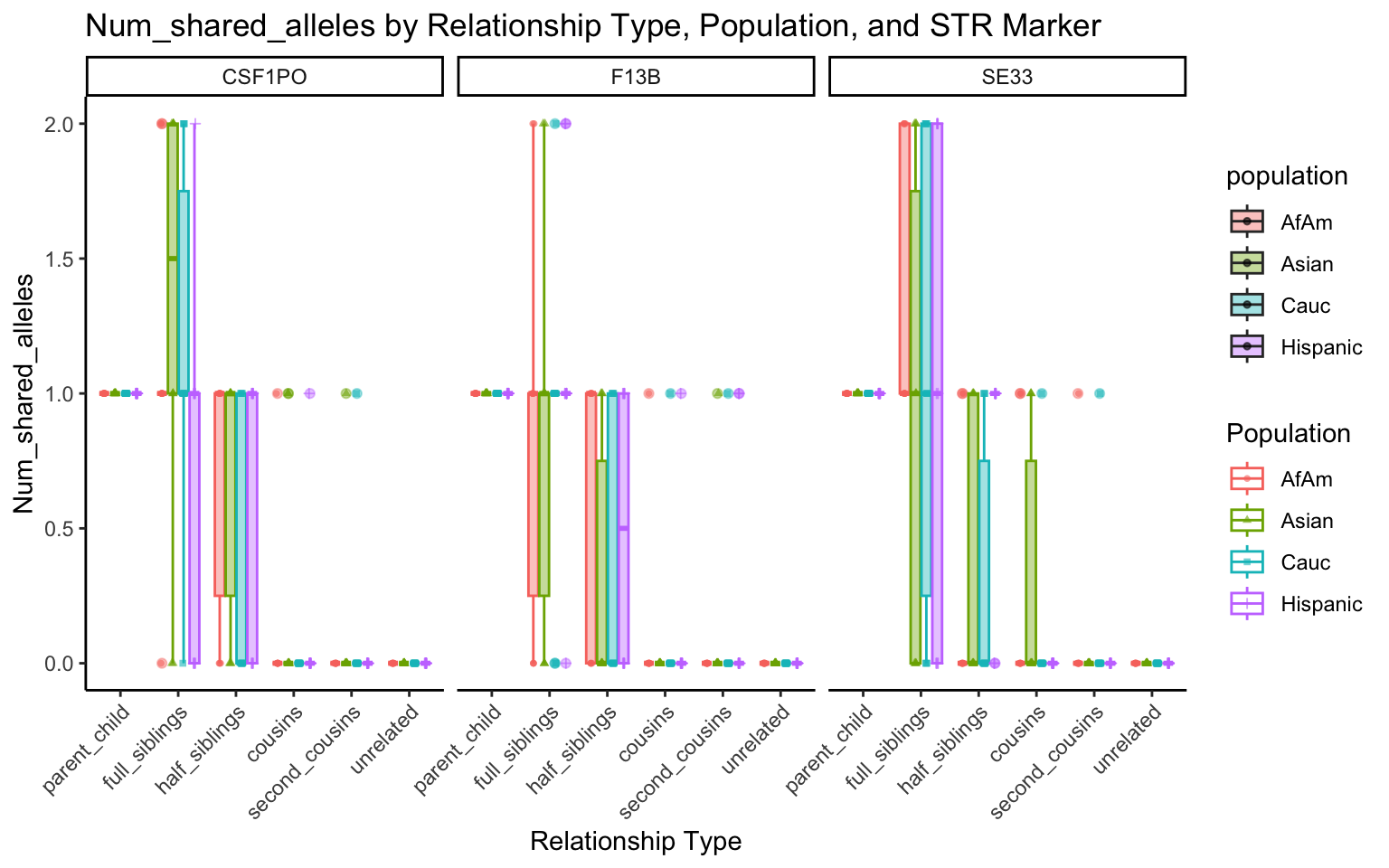
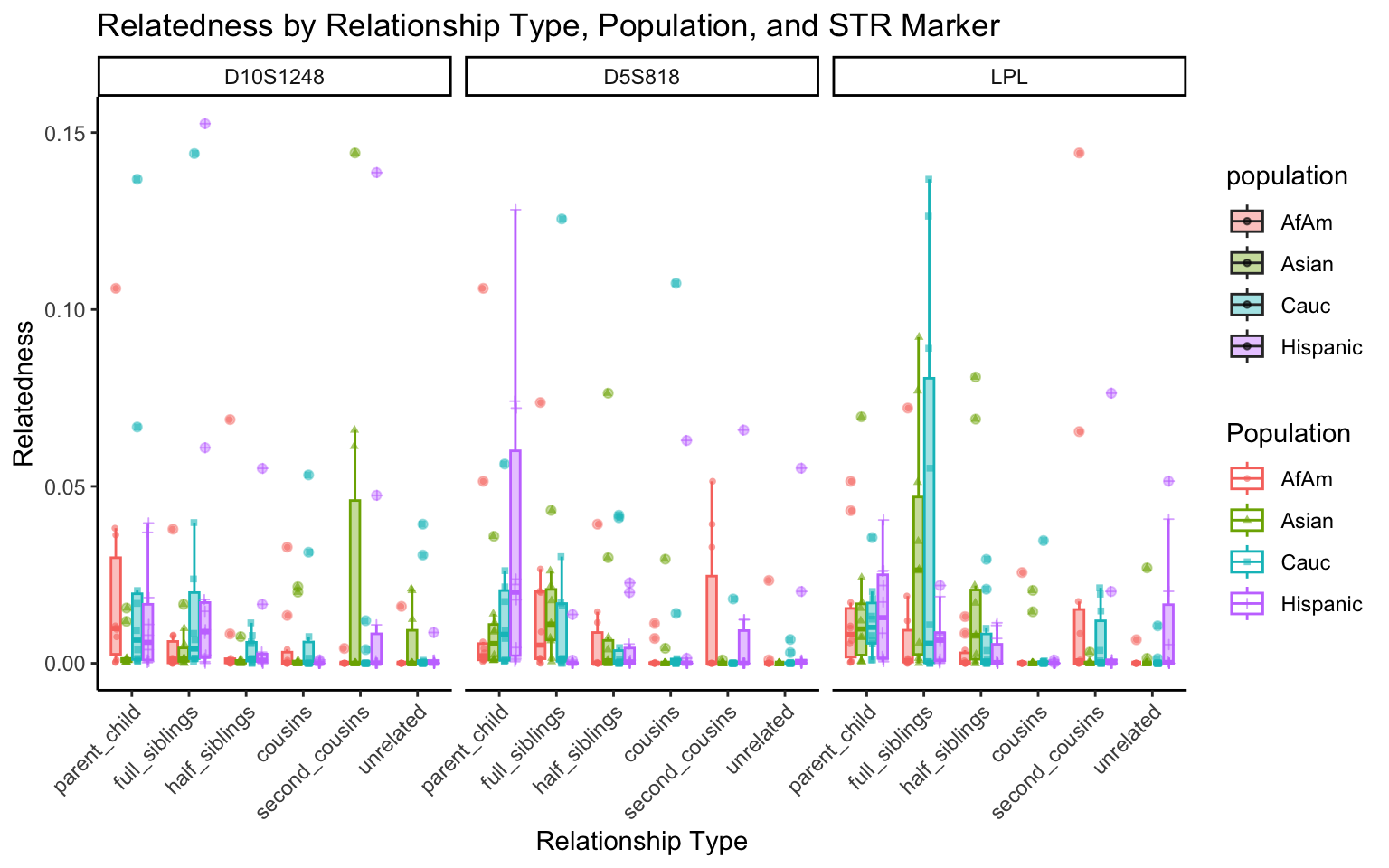
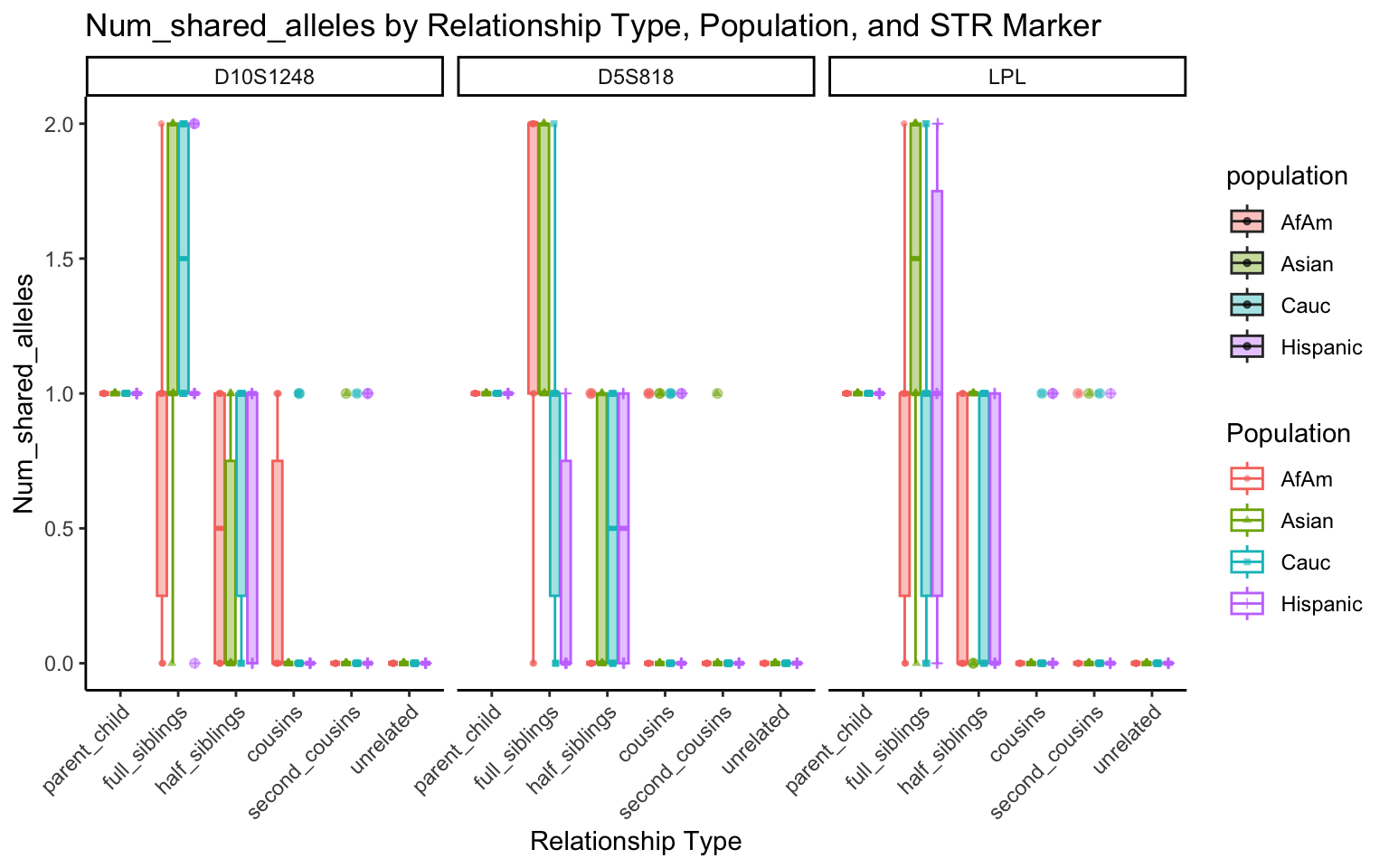
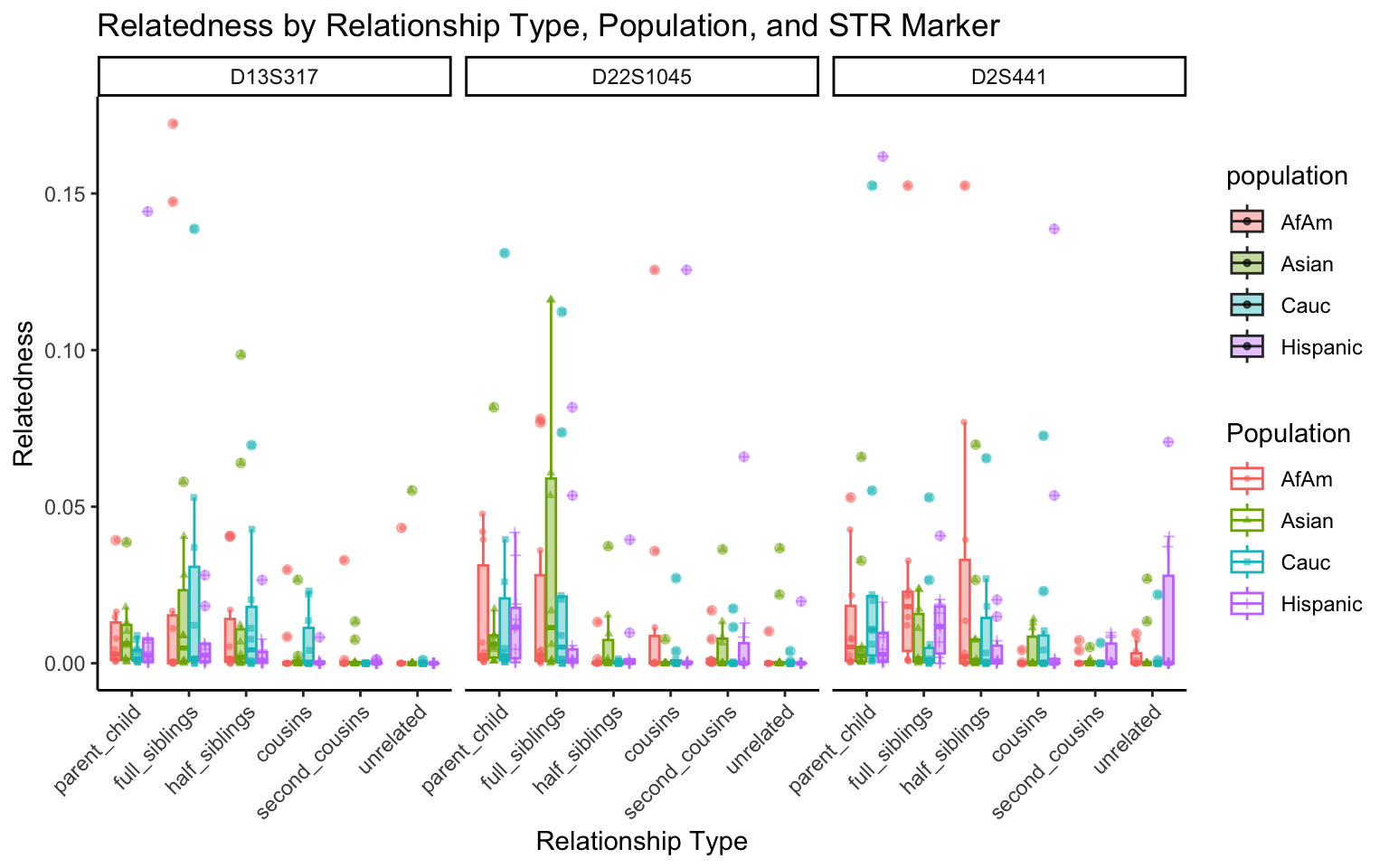
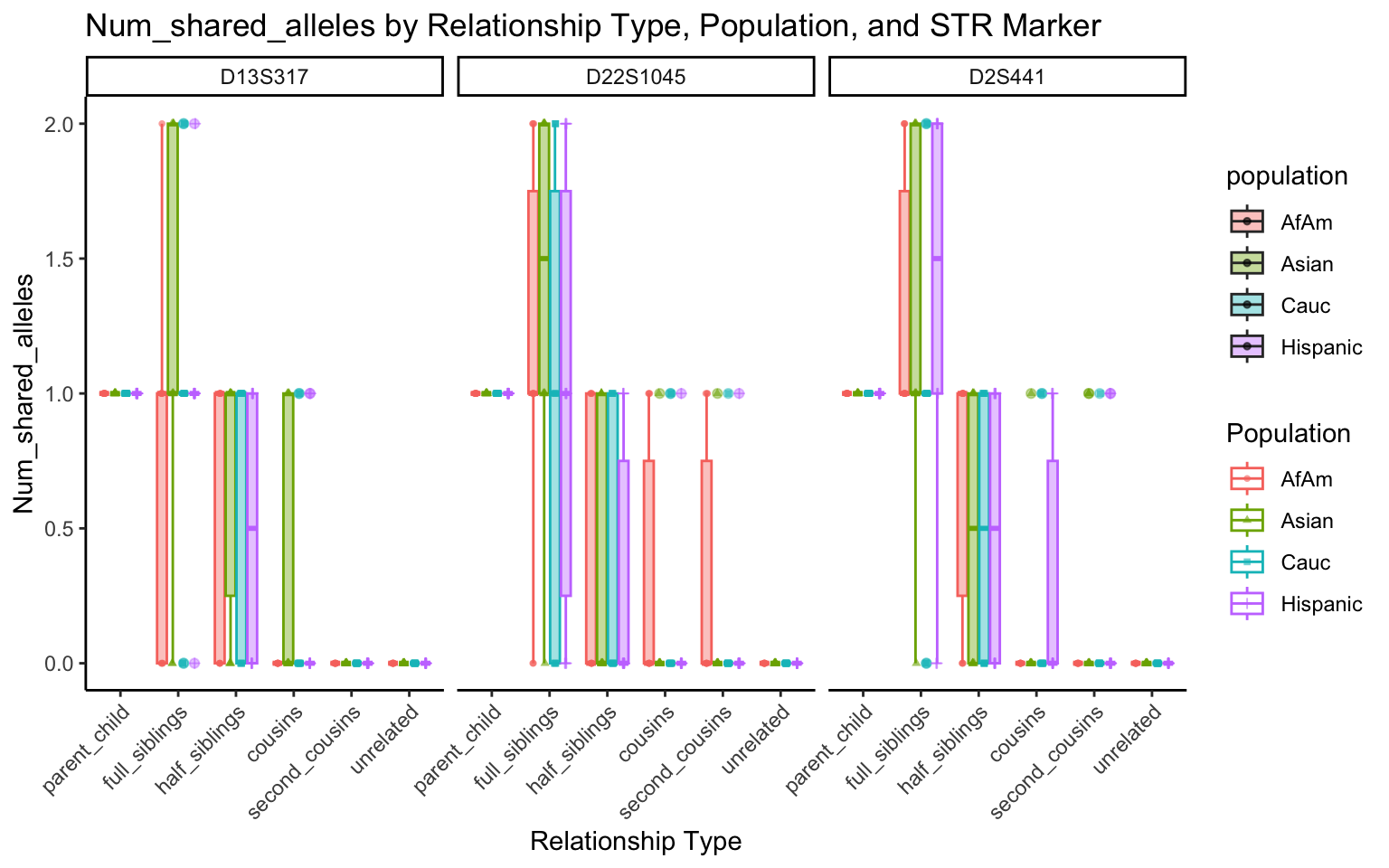
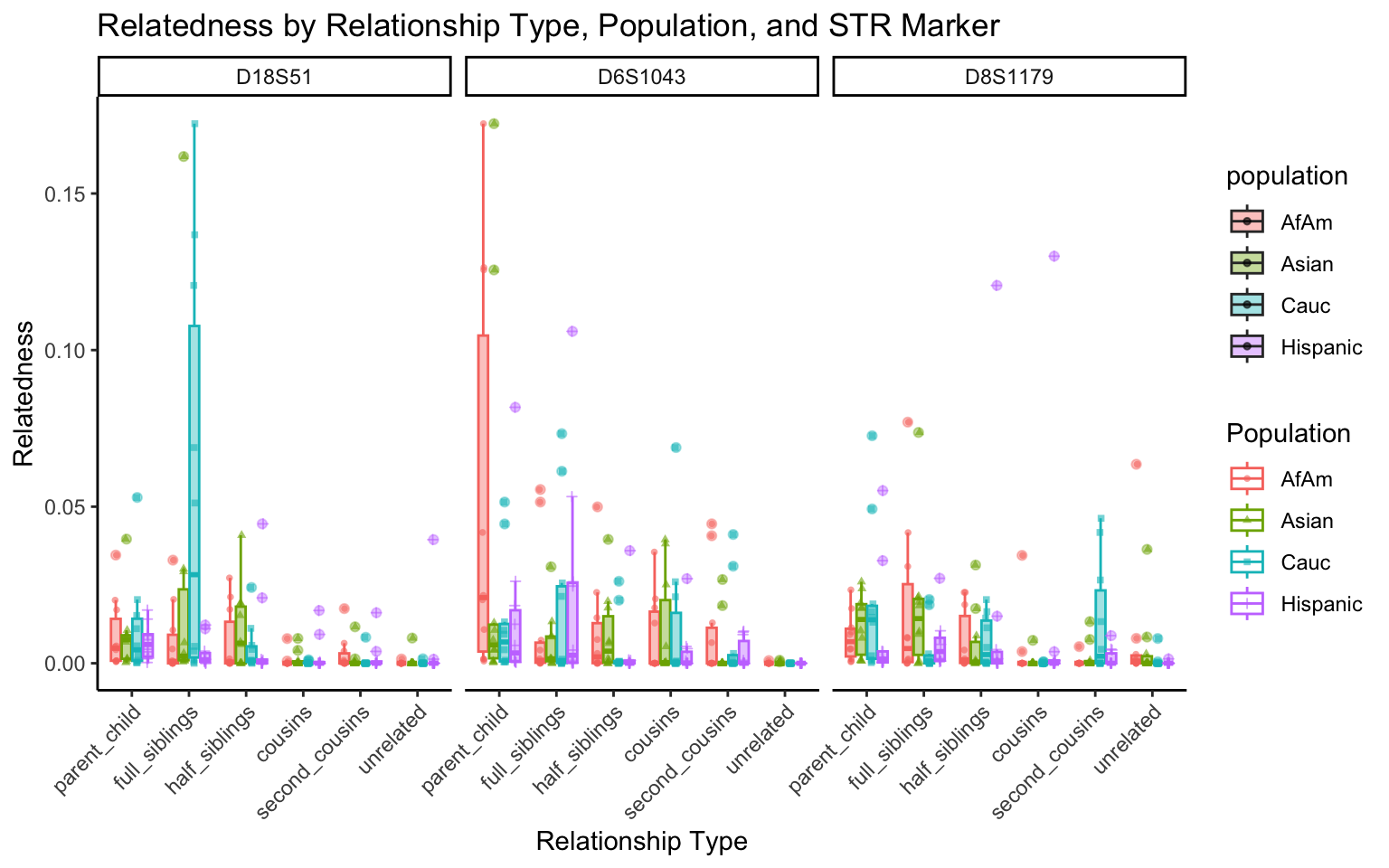
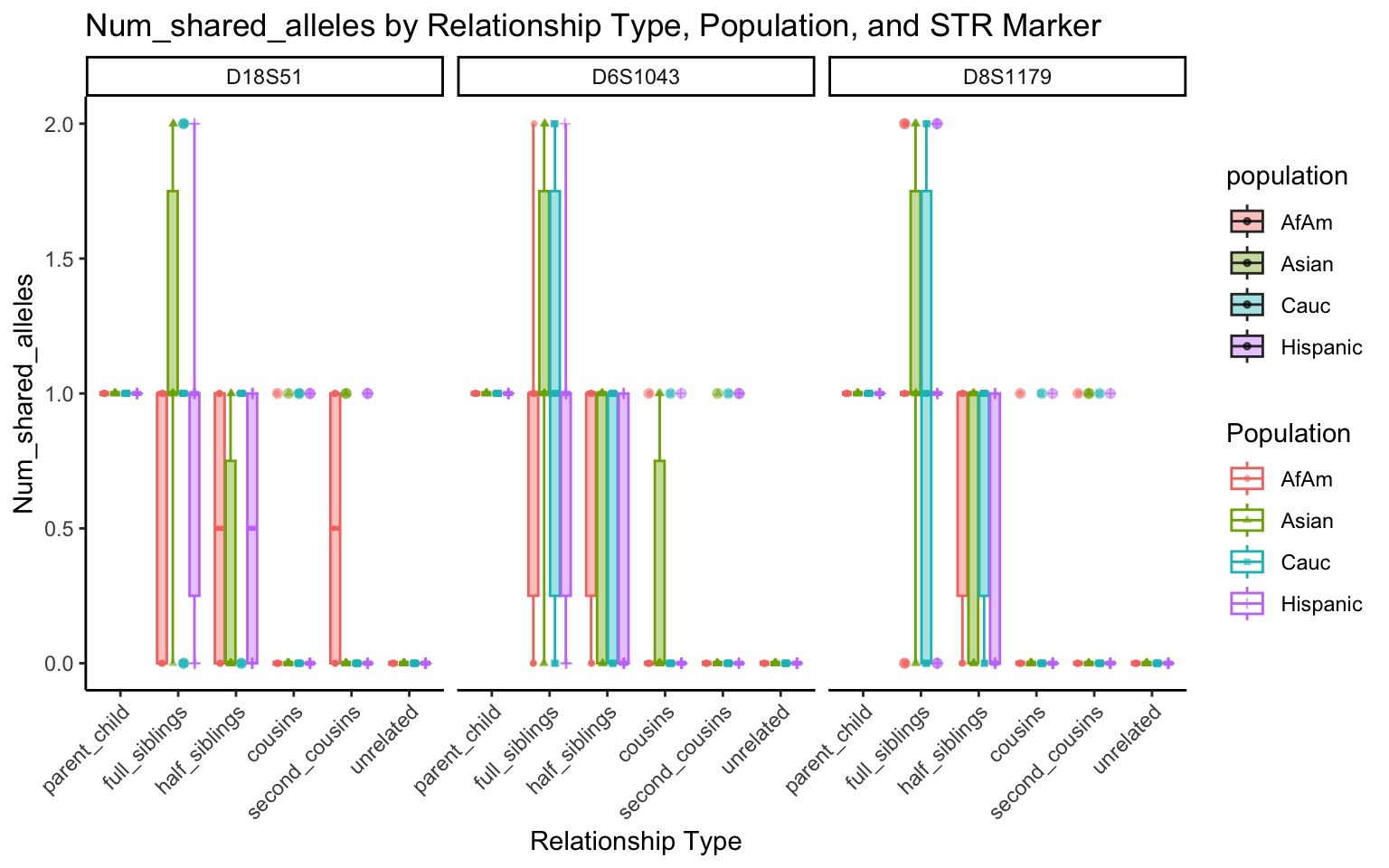
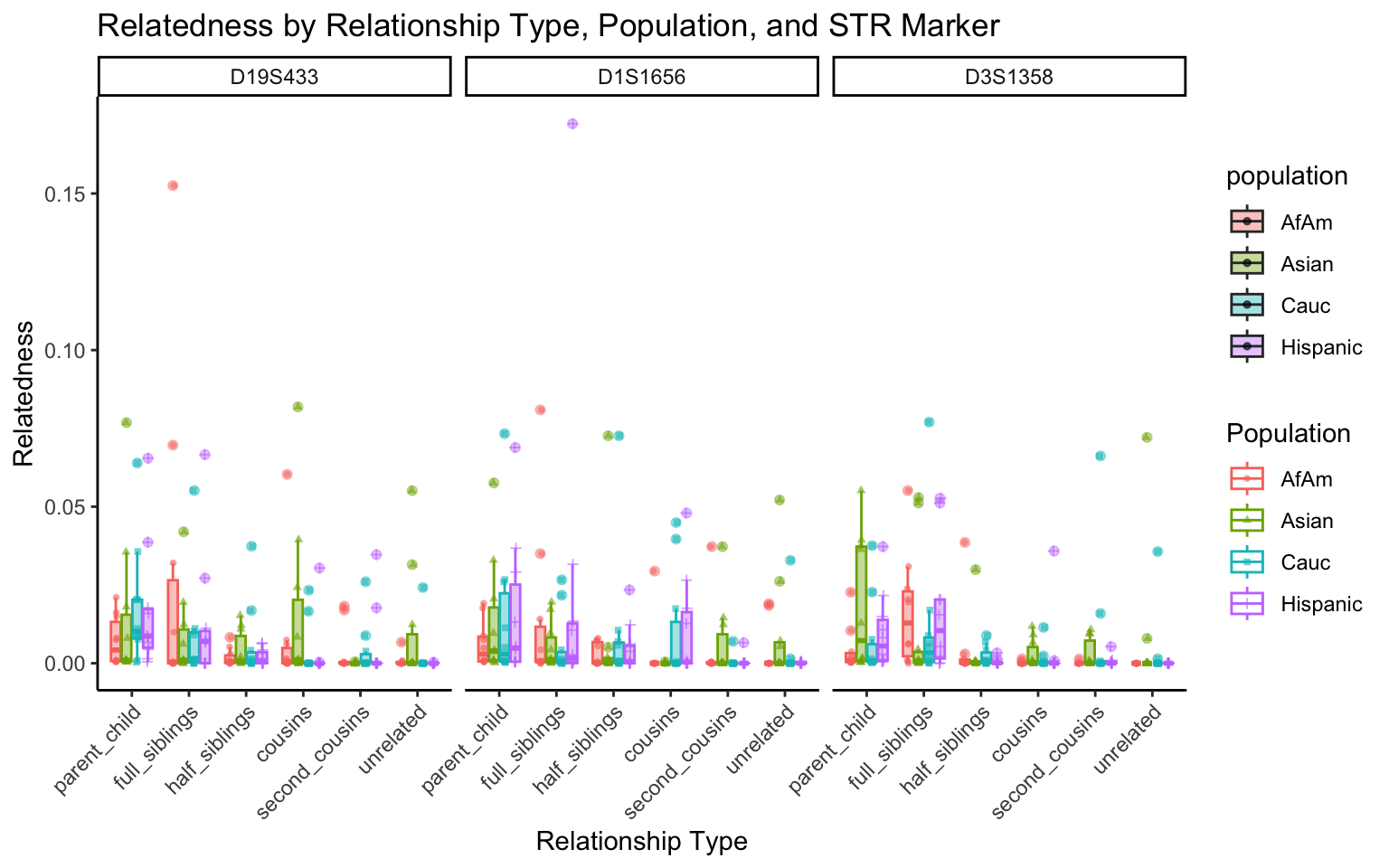
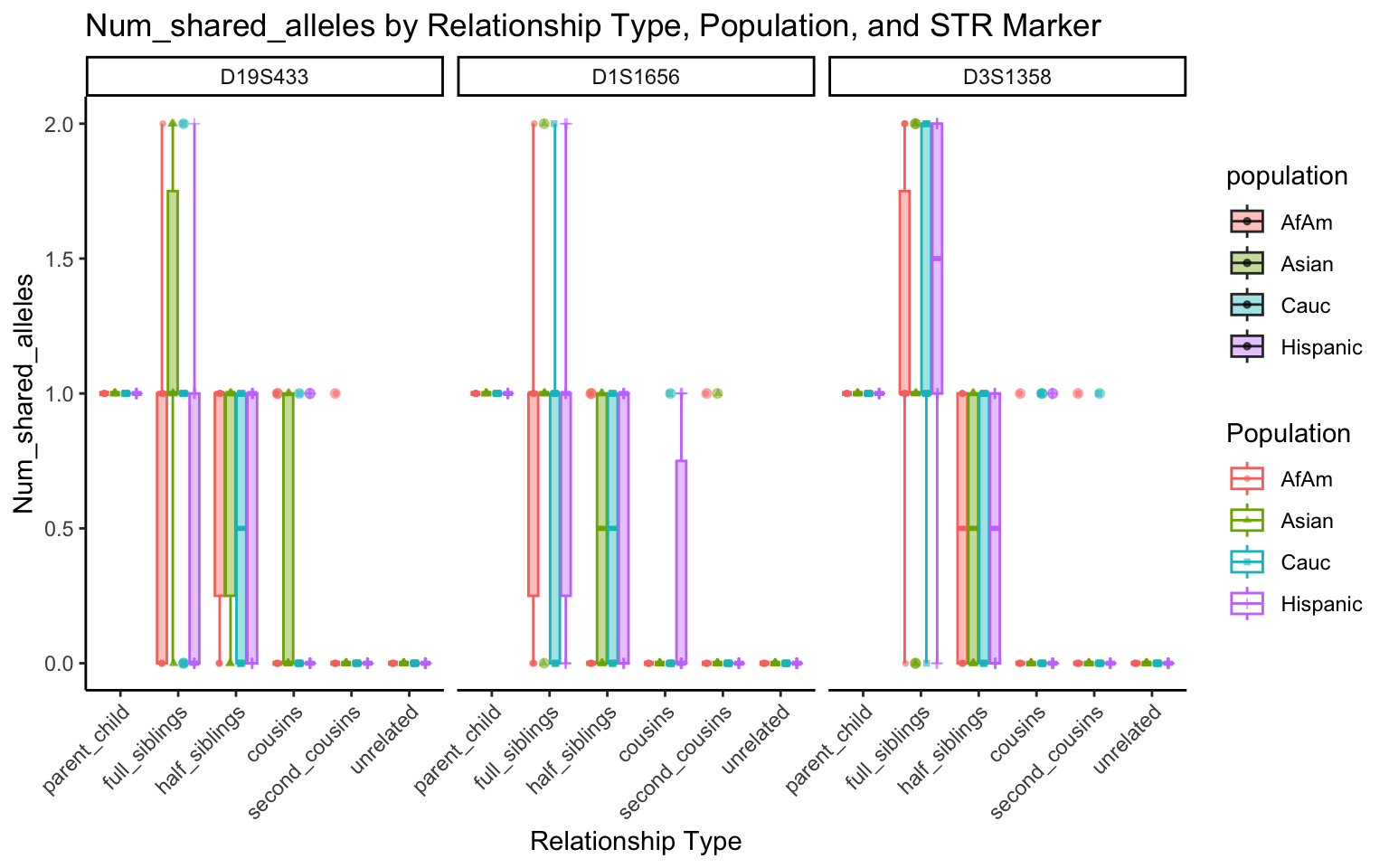
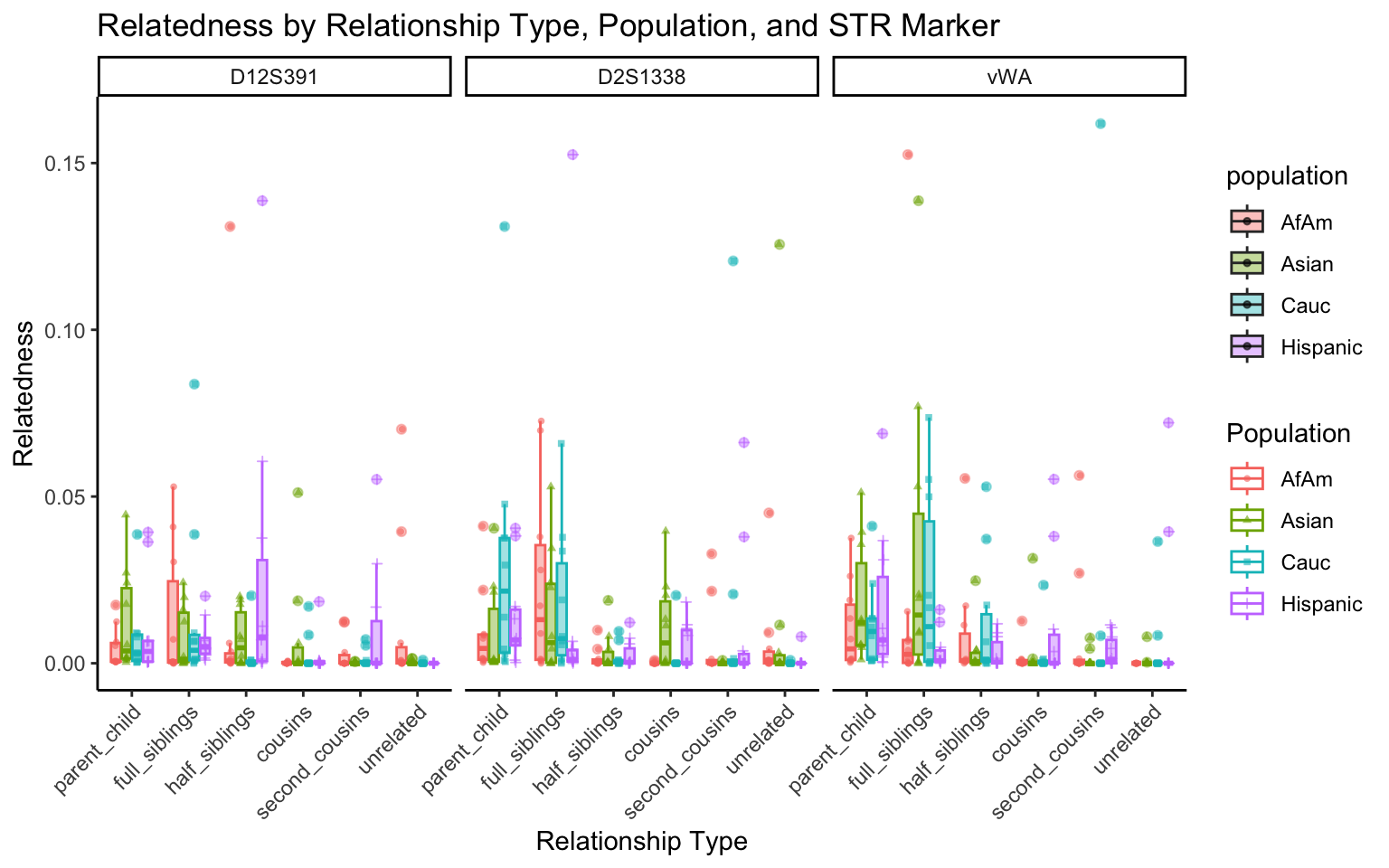
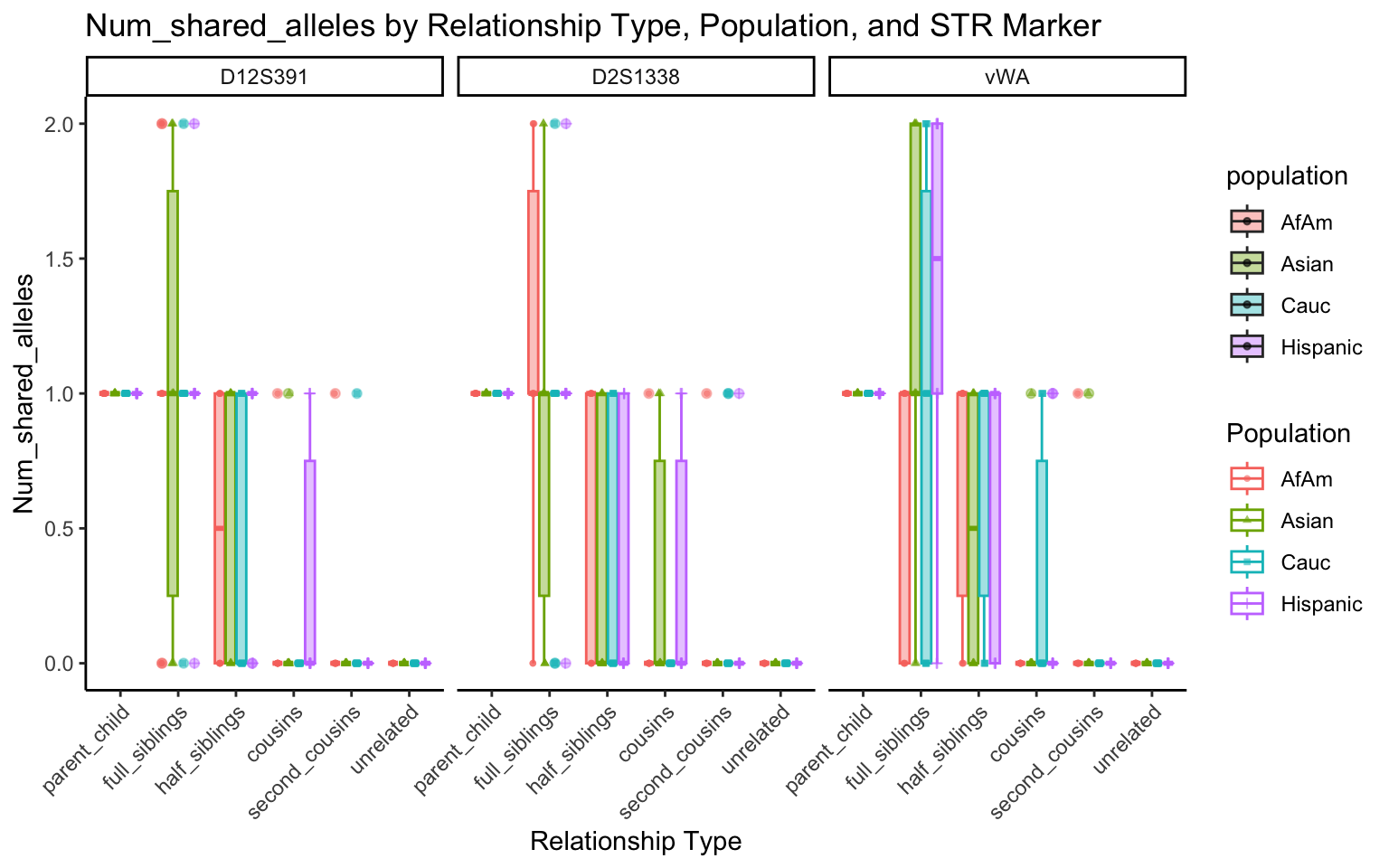
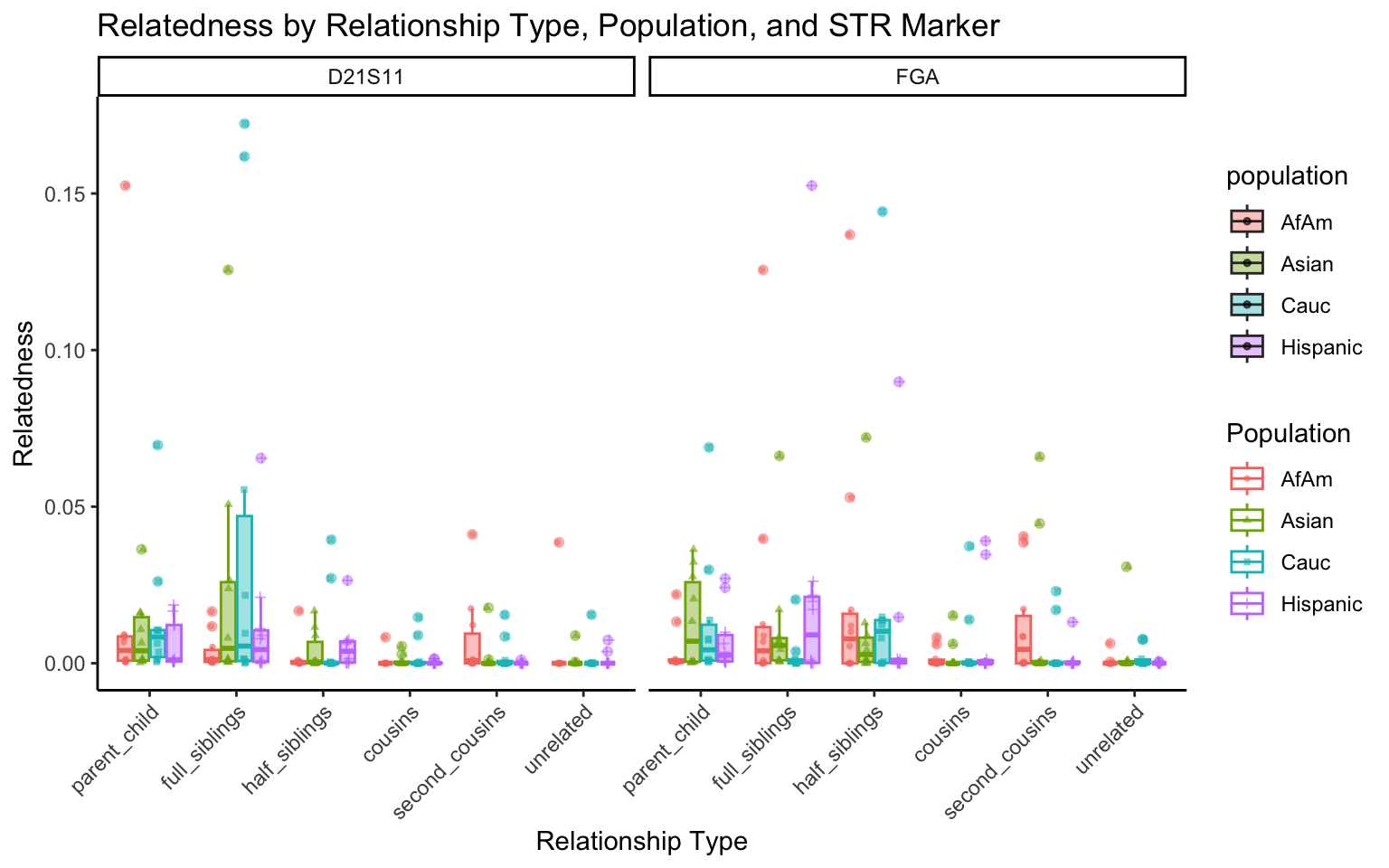
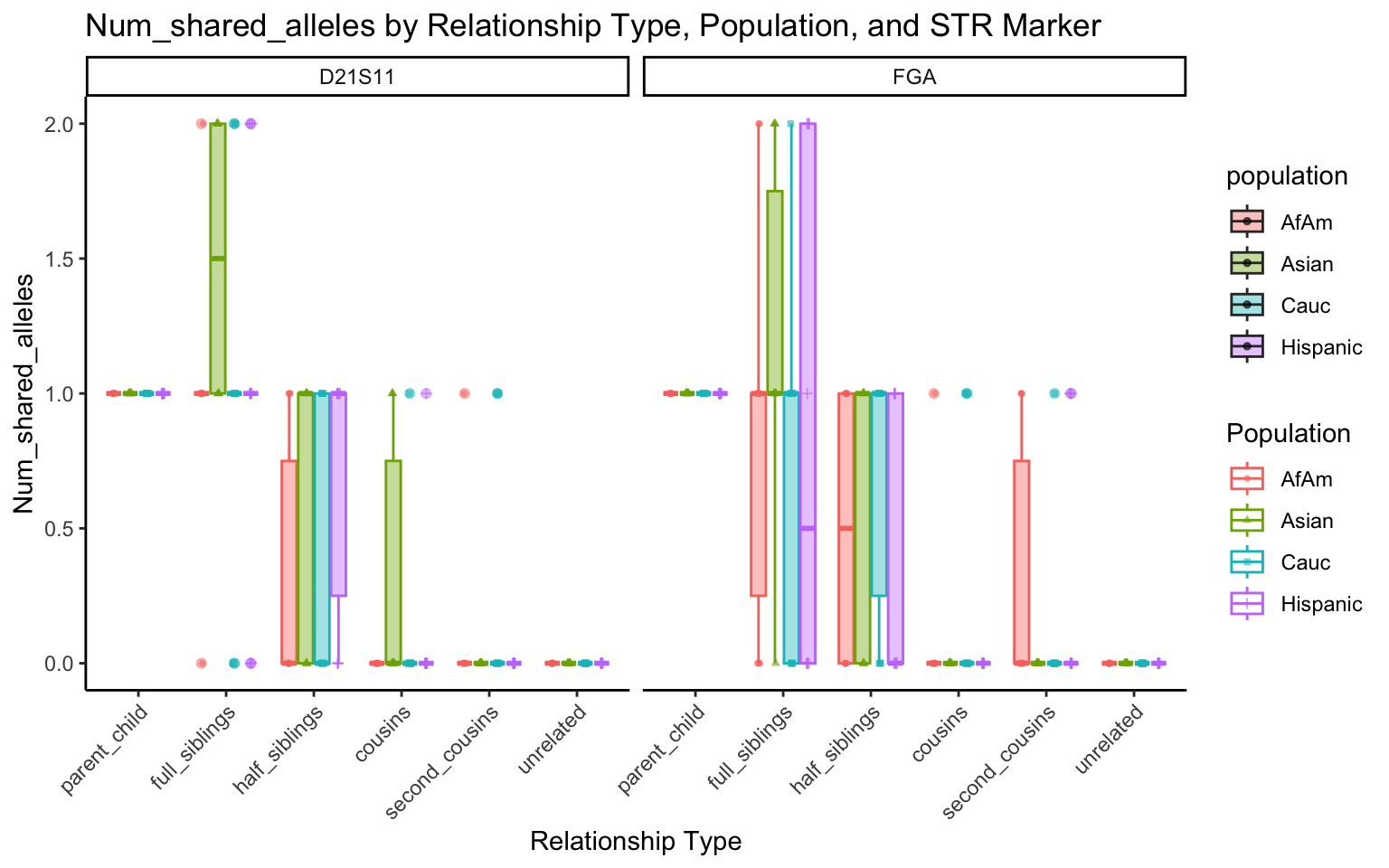
All Markers together
# Function to simulate genotypes for a pair of individuals for all markers
simulate_genotypes_all_markers <- function(df, relationship_type, population) {
markers <- unique(df$marker)
# Simulate the first individual's alleles by drawing from the population frequency for each marker
individual1 <- setNames(lapply(markers, function(marker) {
allele_frequencies <- df %>%
filter(marker == marker, population == population) %>%
pull(frequency) %>%
setNames(df$allele)
sample(names(allele_frequencies), size = 2, replace = TRUE, prob = allele_frequencies)
}), markers)
# Relationship probabilities
relationship_probs <- list(
'parent_child' = c(0, 1, 0),
'full_siblings' = c(1/4, 1/2, 1/4),
'half_siblings' = c(1/2, 1/2, 0),
'cousins' = c(7/8, 1/8, 0),
'second_cousins' = c(15/16, 1/16, 0),
'unrelated' = c(1, 0, 0)
)
prob_shared_alleles <- relationship_probs[[relationship_type]]
num_shared_alleles <- sample(c(0, 1, 2), size = 1, prob = prob_shared_alleles)
individual2 <- setNames(lapply(markers, function(marker) {
allele_frequencies <- df %>%
filter(marker == marker, population == population) %>%
arrange(marker, allele) %>%
pull(frequency) %>%
setNames(df$allele)
prob_shared_alleles <- relationship_probs[[relationship_type]]
non_zero_indices <- which(prob_shared_alleles != 0)
num_shared_alleles <- sample(non_zero_indices - 1, size = 1, prob = prob_shared_alleles[non_zero_indices])
alleles_from_individual1 <- sample(individual1[[marker]], size = num_shared_alleles)
alleles_from_population <- sample(names(allele_frequencies), size = 2 - num_shared_alleles, replace = TRUE, prob = allele_frequencies)
return(c(alleles_from_individual1, alleles_from_population))
}), markers)
# Return the simulated genotypes
return(list(individual1 = individual1, individual2 = individual2))
}
# Function to calculate the index of relatedness for all markers
calculate_relatedness_all_markers <- function(simulated_genotypes, df, population) {
markers <- names(simulated_genotypes$individual1)
# Calculate the number of shared alleles for each marker
num_shared_alleles <- sapply(markers, function(marker) {
sum(simulated_genotypes$individual1[[marker]] %in% simulated_genotypes$individual2[[marker]])
})
# Calculate the index of relatedness as the number of shared alleles weighted inversely to their frequencies
# Now considering both individuals' alleles for the inverse frequency weighting
relatedness <- sapply(markers, function(marker) {
allele_frequencies <- df %>%
filter(marker == marker, population == population) %>%
pull(frequency) %>%
setNames(df$allele)
num_shared_alleles[marker] / (sum(1 / allele_frequencies[simulated_genotypes$individual1[[marker]]]) + sum(1 / allele_frequencies[simulated_genotypes$individual2[[marker]]]))
})
# Return the index of relatedness
return(list(relatedness = relatedness, num_shared_alleles = num_shared_alleles))
}
# Function to simulate genotypes and calculate relatedness for different relationships for all markers
simulate_relatedness_all_markers <- function(df, relationship_type, population) {
# Simulate genotypes for all markers
simulated_genotypes <- simulate_genotypes_all_markers(df, relationship_type, population)
# Calculate and return the relatedness for all markers
relatedness_data <- calculate_relatedness_all_markers(simulated_genotypes, df, population)
# Before returning the results_df, add marker and population information
results_df$marker <- rownames(results_df)
results_df$population <- population
return(relatedness_data)
}Visualizations
# Define the list of relationship types
relationship_types <- c('parent_child', 'full_siblings', 'half_siblings', 'cousins', 'second_cousins', 'unrelated')
# Create a dataframe of all combinations of populations and relationship types
combinations <- expand.grid(population = unique(df$population), relationship_type = relationship_types)
# Apply the function to each combination
results <- combinations %>%
split(seq(nrow(.))) %>%
map_dfr(function(combination) {
population <- combination$population
relationship_type <- combination$relationship_type
# cat("Processing:", "population =", population, "; relationship_type =", relationship_type, "\n")
sim_results <- simulate_relatedness_all_markers(df, relationship_type[[1]], population[[1]])
# Bind resulting data frames
tibble(
population = population,
relationship_type = relationship_type,
sim_results = list(sim_results)
)
})
multi_results <- results %>%
mutate(
sum_relatedness = map_dbl(sim_results, function(x) {
sum(x[["relatedness"]], na.rm = TRUE)
}),
sum_alleles = map_dbl(sim_results, function(x) {
sum(x[["num_shared_alleles"]], na.rm = TRUE)
})
) %>%
select(-sim_results)
multi_results# A tibble: 30 × 4
population relationship_type sum_relatedness sum_alleles
<fct> <fct> <dbl> <dbl>
1 all parent_child 0.339 32
2 AfAm parent_child 0.255 31
3 Cauc parent_child 0.142 34
4 Hispanic parent_child 0.166 30
5 Asian parent_child 0.313 33
6 all full_siblings 0.339 35
7 AfAm full_siblings 0.325 39
8 Cauc full_siblings 0.401 39
9 Hispanic full_siblings 0.306 25
10 Asian full_siblings 0.223 27
# ℹ 20 more rows# Define the number of simulations
n_sims <- 10
# Define the list of relationship types
relationship_types <- c('parent_child', 'full_siblings', 'half_siblings', 'cousins', 'second_cousins', 'unrelated')
# Create a dataframe of all combinations of populations, relationship types, and simulations
combinations <- expand.grid(population = unique(df$population), relationship_type = relationship_types, simulation = 1:n_sims)
# Apply the function to each combination
results <- combinations %>%
split(seq(nrow(.))) %>%
map_dfr(function(combination) {
population <- combination$population
relationship_type <- combination$relationship_type
sim <- combination$simulation
# cat("Processing:", "population =", population, "; relationship_type =", relationship_type, "; simulation =", sim, "\n")
sim_results <- simulate_relatedness_all_markers(df, relationship_type[[1]], population[[1]])
# Bind resulting data frames
tibble(
population = population,
relationship_type = relationship_type,
simulation = sim,
sim_results = list(sim_results)
)
})
multi_results <- results %>%
mutate(
sum_relatedness = map_dbl(sim_results, function(x) {
sum(x[["relatedness"]], na.rm = TRUE)
}),
sum_alleles = map_dbl(sim_results, function(x) {
sum(x[["num_shared_alleles"]], na.rm = TRUE)
})
) %>%
select(-sim_results)
multi_results# A tibble: 300 × 5
population relationship_type simulation sum_relatedness sum_alleles
<fct> <fct> <int> <dbl> <dbl>
1 all parent_child 1 0.581 35
2 AfAm parent_child 1 0.237 31
3 Cauc parent_child 1 0.239 31
4 Hispanic parent_child 1 0.263 32
5 Asian parent_child 1 0.224 29
6 all full_siblings 1 0.409 26
7 AfAm full_siblings 1 0.479 35
8 Cauc full_siblings 1 0.230 28
9 Hispanic full_siblings 1 0.280 26
10 Asian full_siblings 1 0.305 32
# ℹ 290 more rowscreate_plot <- function(df, variable_to_plot) {
# Create the plot
p <- ggplot(df, aes(x = relationship_type, y = .data[[variable_to_plot]], color = population, shape = population, fill = population)) +
geom_boxplot(alpha = 0.4, position = position_dodge(width = 0.75)) +
geom_point(position = position_jitterdodge(jitter.width = 0.1, dodge.width = 0.75), size = 1, alpha = 0.6) +
theme_classic() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
scale_x_discrete(limits = c('parent_child', 'full_siblings', 'half_siblings', 'cousins', 'second_cousins', 'unrelated')) +
labs(title = paste(ucfirst(variable_to_plot), "by Relationship Type and Population"),
x = "Relationship Type",
y = ucfirst(variable_to_plot),
color = "Population",
shape = "Population")
return(p)
}# Filter your data for unique STR markers and remove the "all" population
df_plt_multi_results <- multi_results %>%
filter(population != "all") %>%
select(-simulation)
p <- create_plot(df_plt_multi_results, "sum_relatedness")
p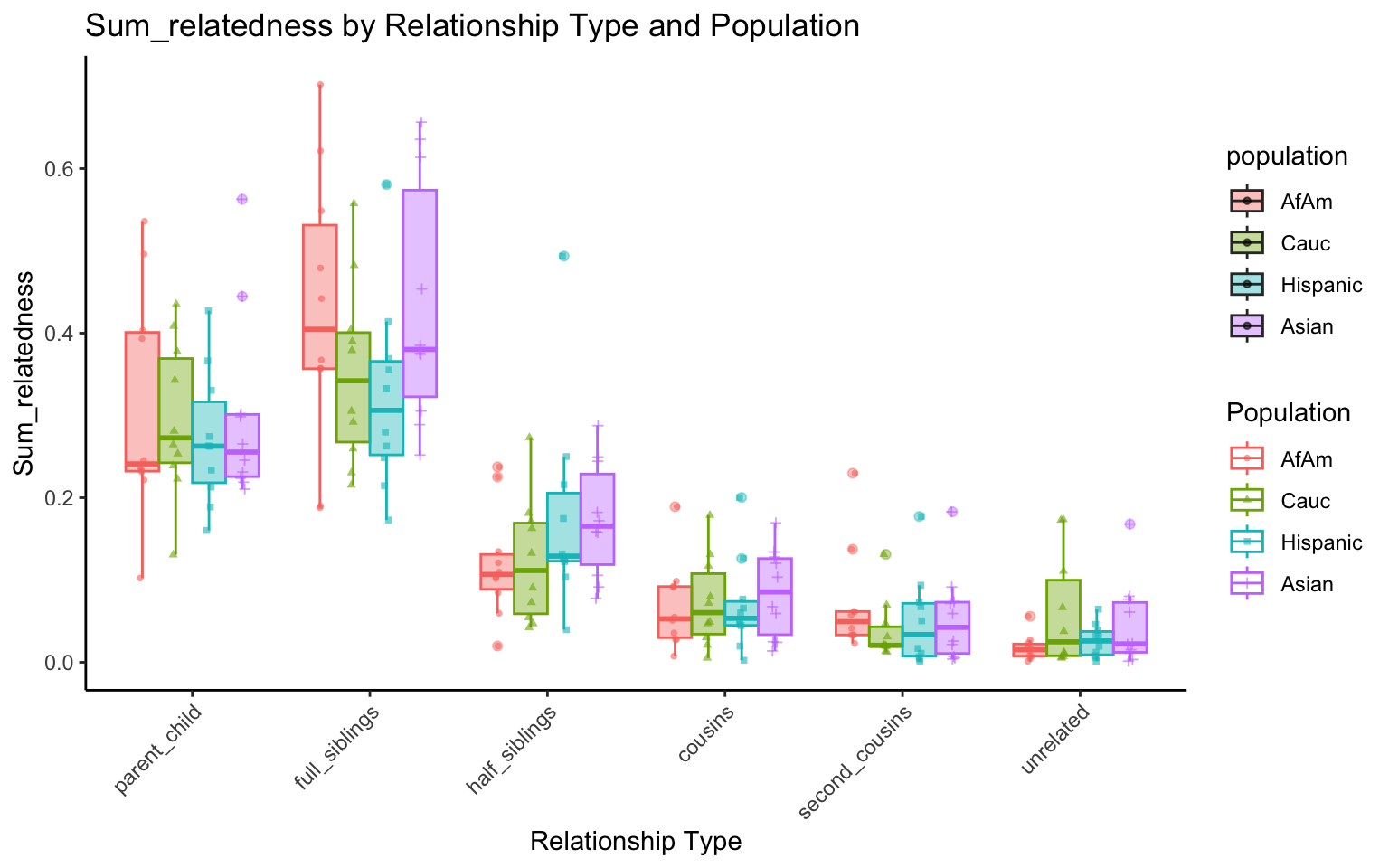
plt_allele <- create_plot(df_plt_multi_results, "sum_alleles")
plt_allele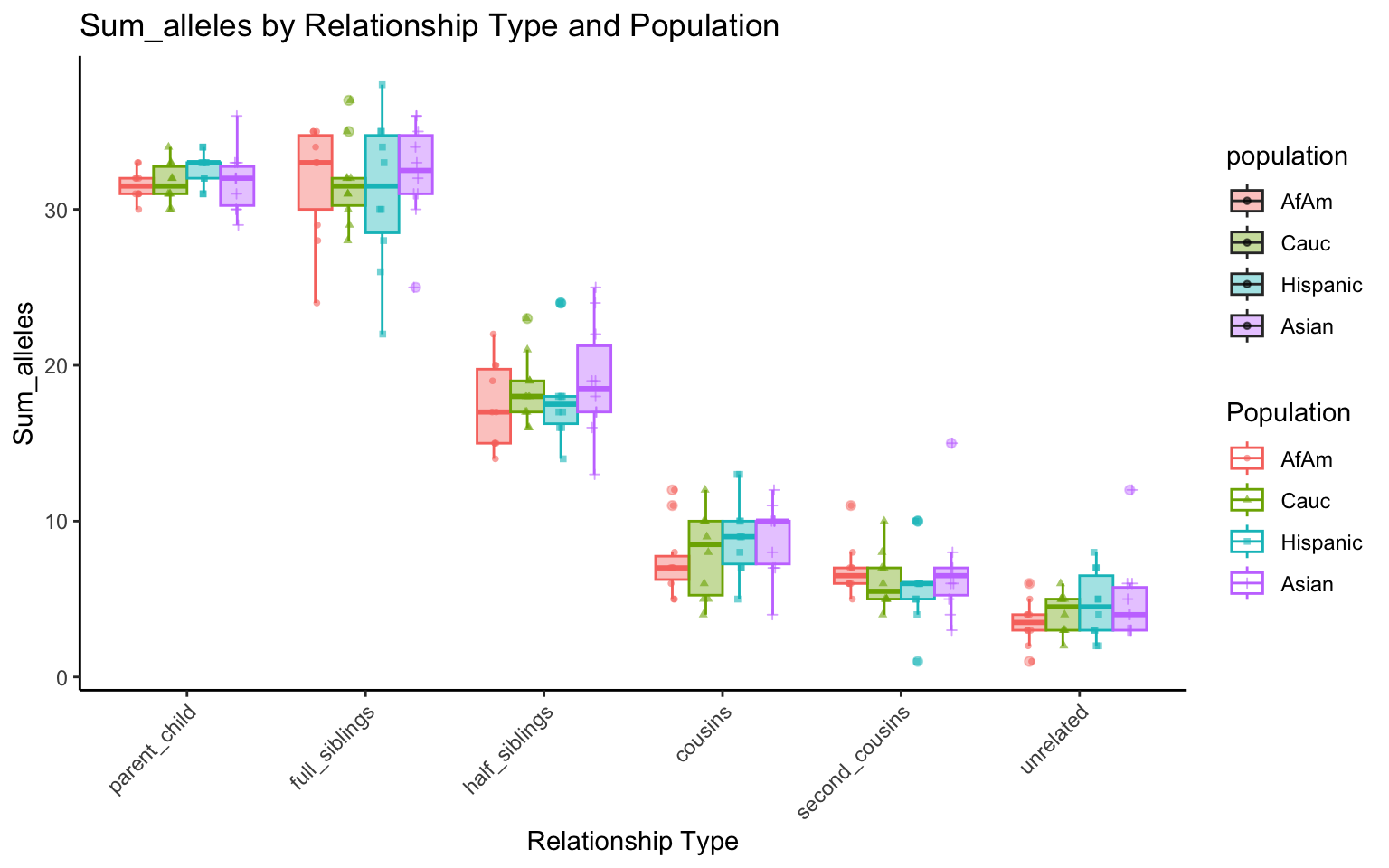
`
Updated LR
From Weight-of-evidence for forensic DNA profiles book
Likelihood ratio for a single locus is:
\[ R=\kappa_0+\kappa_1 / R_X^p+\kappa_2 / R_X^u \] Where \(\kappa\) is the probability of having 0, 1 or 2 alleles IBD for a given relationship.
The \(R_X\) terms are quantifying the “surprisingness” of a particular pattern of allele sharing.
The \(R_X^p\) terms attached to the \(kappa_1\) are defined in the following table:
\[ \begin{aligned} &\text { Table 7.2 Single-locus LRs for paternity when } \mathcal{C}_M \text { is unavailable. }\\ &\begin{array}{llc} \hline c & Q & R_X \times\left(1+2 F_{S T}\right) \\ \hline \mathrm{AA} & \mathrm{AA} & 3 F_{S T}+\left(1-F_{S T}\right) p_A \\ \mathrm{AA} & \mathrm{AB} & 2\left(2 F_{S T}+\left(1-F_{S T}\right) p_A\right) \\ \mathrm{AB} & \mathrm{AA} & 2\left(2 F_{S T}+\left(1-F_{S T}\right) p_A\right) \\ \mathrm{AB} & \mathrm{AC} & 4\left(F_{S T}+\left(1-F_{S T}\right) p_A\right) \\ \mathrm{AB} & \mathrm{AB} & 4\left(F_{S T}+\left(1-F_{S T}\right) p_A\right)\left(F_{S T}+\left(1-F_{S T}\right) p_B\right) /\left(2 F_{S T}+\left(1-F_{S T}\right)\left(p_A+p_B\right)\right) \\ \hline \end{array} \end{aligned} \]
For our purposes we will take out the \(F_{S T}\) values. So the table will be as follows:
\[ \begin{aligned} &\begin{array}{llc} \hline c & Q & R_X \\ \hline \mathrm{AA} & \mathrm{AA} & p_A \\ \mathrm{AA} & \mathrm{AB} & 2 p_A \\ \mathrm{AB} & \mathrm{AA} & 2p_A \\ \mathrm{AB} & \mathrm{AC} & 4p_A \\ \mathrm{AB} & \mathrm{AB} & 4 p_A p_B/(p_A+p_B) \\ \hline \end{array} \end{aligned} \]
If none of the alleles match, then the \(\kappa_1 / R_X^p = 0\).
The \(R_X^u\) terms attached to the \(kappa_2\) are defined as:
If both alleles match and are homozygous the equation is 6.4 (pg 85). Single locus match probability: \(\mathrm{CSP}=\mathcal{G}_Q=\mathrm{AA}\) \[ \frac{\left(2 F_{S T}+\left(1-F_{S T}\right) p_A\right)\left(3 F_{S T}+\left(1-F_{S T}\right) p_A\right)}{\left(1+F_{S T}\right)\left(1+2 F_{S T}\right)} \] Simplified to: \[ p_A{ }^2 \]
If both alleles match and are heterozygous, the equation is 6.5 (pg 85) Single locus match probability: \(\mathrm{CSP}=\mathcal{G}_Q=\mathrm{AB}\) \[ 2 \frac{\left(F_{S T}+\left(1-F_{S T}\right) p_A\right)\left(F_{S T}+\left(1-F_{S T}\right) p_B\right)}{\left(1+F_{S T}\right)\left(1+2 F_{S T}\right)} \] Simplified to:
\[ 2 p_A p_B \] If both alleles do not match then \(\kappa_2 / R_X^u = 0\).
Calculating LR
We need 100,000 unrelated pairs.
sessionInfo()R version 4.4.1 (2024-06-14)
Platform: x86_64-apple-darwin20
Running under: macOS Sonoma 14.6.1
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-x86_64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.0
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
time zone: America/Detroit
tzcode source: internal
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] kableExtra_1.4.0 knitr_1.48 data.table_1.15.4 lubridate_1.9.3
[5] forcats_1.0.0 stringr_1.5.1 dplyr_1.1.4 purrr_1.0.2
[9] readr_2.1.5 tidyr_1.3.1 tibble_3.2.1 ggplot2_3.5.1
[13] tidyverse_2.0.0 readxl_1.4.3 workflowr_1.7.1
loaded via a namespace (and not attached):
[1] gtable_0.3.5 xfun_0.45 bslib_0.7.0 processx_3.8.4
[5] callr_3.7.6 tzdb_0.4.0 vctrs_0.6.5 tools_4.4.1
[9] ps_1.7.7 generics_0.1.3 fansi_1.0.6 highr_0.11
[13] pkgconfig_2.0.3 rematch_2.0.0 lifecycle_1.0.4 compiler_4.4.1
[17] farver_2.1.2 git2r_0.33.0 munsell_0.5.1 getPass_0.2-4
[21] httpuv_1.6.15 htmltools_0.5.8.1 sass_0.4.9 yaml_2.3.9
[25] later_1.3.2 pillar_1.9.0 jquerylib_0.1.4 whisker_0.4.1
[29] cachem_1.1.0 tidyselect_1.2.1 digest_0.6.36 stringi_1.8.4
[33] labeling_0.4.3 rprojroot_2.0.4 fastmap_1.2.0 grid_4.4.1
[37] colorspace_2.1-0 cli_3.6.3 magrittr_2.0.3 utf8_1.2.4
[41] withr_3.0.0 scales_1.3.0 promises_1.3.0 timechange_0.3.0
[45] rmarkdown_2.27 httr_1.4.7 cellranger_1.1.0 hms_1.1.3
[49] evaluate_0.24.0 viridisLite_0.4.2 rlang_1.1.4 Rcpp_1.0.12
[53] glue_1.7.0 xml2_1.3.6 svglite_2.1.3 rstudioapi_0.16.0
[57] jsonlite_1.8.8 R6_2.5.1 systemfonts_1.1.0 fs_1.6.4